mathepanik.de

Lektion
Kreise: Bögen und Sektoren

Kreisumfang und Kreisfläche

1.1	Gegeben ein Kreis mit Radius 10 cm. Berechne Umfang und Flächeninhalt.	Lösung u = π · 2 · 10 = 62,83 cm A = π · 10² = 314 cm²

1.2	Gegeben ein Kreis mit Radius 7 cm. Berechne Umfang und Flächeninhalt.	Lösung u = π · 2 · 7 = 43,98 cm A = π · 7² = 153,94 cm²

1.3	Ein Kreis hat einen Umfang von 20 cm. Berechne Radius und Flächeninhalt.	Lösung 20 = π · 2 · r \| : π : 2 r = 3,18 cm A = π · 3,18² = 31,77 cm²

1.4	Ein Kreis hat einen Umfang von 1 m. Berechne Radius und Flächeninhalt.	Lösung 1 = π · 2 · r \| : π : 2 r = 0,16 m A = π · 0,16² = 0,08 m²

1.5	Ein Kreis hat einen Flächeninhalt von 100 cm². Berechne den Umfang.	Lösung 100 = π · r² \| : π 31,83 = r² \| √ r = 5,64 cm u = π · 2 · 5,64 = 35,44 cm

1.6	Ein Kreis hat einen Flächeninhalt von 5 m². Berechne den Umfang.	Lösung 5 = π · r² \| : π 1,59 = r² \| √ r = 1,26 m u = π · 2 · 1,26 = 7,92 m

Kreisringe

2.1	Zwei konzentrische Kreise besitzen die Radien 3 cm und 7 cm. Berechne den Flächeninhalt des Ringes.	Lösung A = π · (7² – 3²) = 125,66 cm²

2.2	Zwei konzentrische Kreise besitzen die Radien 10 cm und 5 cm. Berechne den Flächeninhalt des Ringes.	Lösung A = π · (10² – 5²) = 235,62 cm²

2.3	Ein Kreisring hat den Flächeninhalt 50 cm². Welchen Radius besitzt der äußere Kreis, wenn der innere einen Radius von 12 cm besitzt?	Lösung 50 = π · (r₁² – 12²) \| : π 15,92 = r₁² – 144 \| + 144 159,92 = r₁² \| √ r₁ = 12,65 cm

2.4	Ein Kreisring hat den Flächeninhalt 100 cm². Welchen Radius besitzt der innere Kreis, wenn der äußere einen Radius von 8 cm besitzt?	Lösung 100 = π · (8² – r₂²) \| : π 31,83 = 64 – r₂² \| – 64 -32,17 = - r₂² \| : (-1) 32,17 = r₂² \| √ r₂ = 5,67 cm

2.5	Ein Kreisring hat den Flächeninhalt 80 cm². Welchen Umfang besitzt der innere Kreis, wenn der äußere einen Radius von 10 cm besitzt?	Lösung 80 = π · (10² – r₂²) \| : π 25,46 = 100 – r₂² \| – 100 -74,54 = - r₂² \| : (-1) 74,54 = r₂² \| √ r₂ = 8,63 cm u₂ = π · 2 · 8,63 = 54,22 cm

Kreisbogen, Kreissektor und Kreissegment

3.1

Ein Kreisbogen von 30° wird aus einem Kreis mit Radius 7 cm herausgeschnitten:

Berechne die Bogenlänge, die Fläche des Sektors und die Fläche des Segments.

Lösung

3.2

Ein Kreisbogen von 120° wird aus einem Kreis mit Radius 15 cm herausgeschnitten:

Berechne die Bogenlänge, die Fläche des Sektors und de Fläche des Segments.

Lösung

3.3

Gegeben ist ein 50 cm langer Kreisbogen eines Kreises mit Durchmesser 24 cm. Berechne die Fläche des zugehörigen Kreissektors.

Lösung

3.4

Gegeben ist ein 120 cm langer Kreisbogen eines Kreises mit Durchmesser 96 cm. Berechne die Fläche des zugehörigen Kreissegments.

Lösung

3.5

Ein Kreissektor mit der Fläche 500 cm² wurde unter einem Winkel von 90° aus einem Kreis heraus geschnitten. Wie groß ist die zugehörige Bogenlänge?

Lösung

Kreissektoren an Drei- und Vierecken

4.1

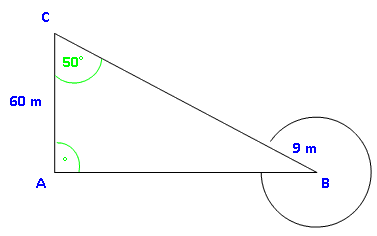
Der Punkt B des Dreiecks ist der Mittelpunkt eines Kreises mit Radius 9 m. Wie groß ist der Flächeninhalt der gesamten Fläche?

Lösung

4.2

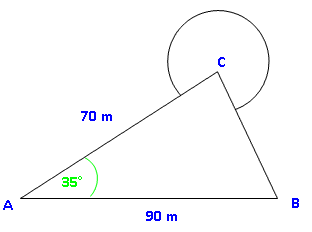
Der Punkt C des Dreiecks ist der Mittelpunkt eines Kreises mit Radius 15 m. Wie groß ist der Flächeninhalt der gesamten Fläche?

Lösung

4.3

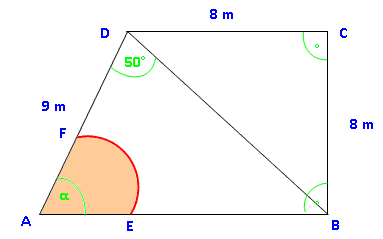
Aus dem Viereck wird bei A ein Kreissektor mit Radius 4 m heraus geschnitten. Wie groß ist die Fläche des Kreissektors im Verhältnis zur Fläche des ursprünglichen Vierecks?

Lösung

Fehler gefunden oder Anregungen?