
Teste dein Wissen
Test 1
Bearbeite die Aufgaben wie gewohnt und kontrolliere dein Ergebnis anhand der Lösung. Anschließend kannst du sie auf einer Prozent-Skala bewerten und deine Note berechnen lassen. Aufgaben, die du nicht bearbeiten möchtest, kannst du mit 'n.w. (nicht werten)' kennzeichnen.
Sinus, Kosinus oder Tangens?
Vervollständige die folgenden Gleichungen.
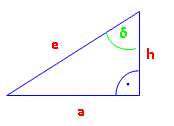
sin δ = cos δ =
tan δ = a2 = |
|
Lösung
sin δ =
cos δ =
tan δ =
a 2 = e 2 – h 2
|
|
Note: |
|
|
|
Winkel berechnen.
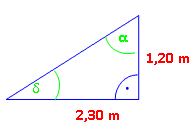
Berechne die beiden fehlenden Winkel.
 |
|
Lösung
tan α =
= 1,92 α = 62,45° δ = 180° – 90° – 62,45° = 27,55°
|
|
Note: |
|
|
|
Seiten berechnen
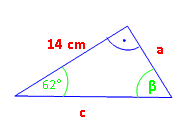
Berechne zunächst eine der beiden fehlenden Seiten über sin, cos oder tan. Die andere Seite dann über Pythagoras und zum Schluss den fehlenden Winkel.
 |
|
Lösung
tan 62° =
| · 14 14 · tan 62° = a a = 26,33 cm c 2 = 14 2 + 26,33 2 | √ c = 29,82 cm β = 180° – 90° – 62° = 28°
|
|
Note: |
|
|
|
Vermischte Aufgaben
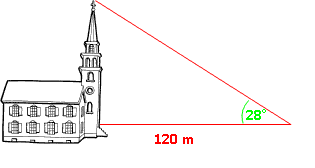
Ein 1,80 m großer Mensch (Augenhöhe 20 cm niedriger) peilt aus 120 m Entfernung die Spitze eines Kirchturmes unter einem Winkel von 28° an.
a) Wie hoch ist der Turm?
b) Wie lange müsste ein Seil sein, das von der Spitze zum Betrachter gespannt wäre? |
|
Lösung
Höhe: tan 28° =
| · 120 h' = 120 · tan 28° = 63,81m Gesamthöhe: 63,81 m + 1,60 = 65,41 m Seil: x 2 = 120 2 + 63,81 2 | √ x = 135,9 m
|
|
Note: |
|
|
|
Tangens bei Geraden im Koordinatensystem
| Bei den folgenden Geraden ist der Steigungswinkel angegeben und ein Punkt, durch den die Gerade verläuft. Gib die Gleichung der Geraden an. |
|
| α = 70° P(-3 | 1) |
|
Lösung
m = tan 70° = 2,75
y = 2,75·x + t P(-3 | 1)
1 = 2,75·(-3) + t | + 8,25
9,25 = t
y = 2,75·x + 9,25
|
|
Note: |
|
|
|








