|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||||||
|
Kein schwieriges Thema: Du würdest es "Vergrößerungen und Verkleinerungen" nennen. Die Mathematiker schaffen es aber auch, hieraus eine große Geheimwissenschaft zu machen! ;O)
Das Thema hat zwei Schwerpunkte: Zunächst einmal geht es darum, zu verstehen, wie man in der Mathematik maßstabsgetreue Vergrößerungen und Verkleinerungen anfertigt. Und welche Eigenschaften das neue Bild hat. Und dann, wesentlich wichtiger, lernen wir in Figuen, die solche Vergrößerungen oder Verkleinerungen enthalten, zu rechnen. (Vierstreckensatz bzw. Strahlensatz) |
 |
|||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Die Idee der zentrischen Streckung | ||||||||||||||||||||||||||||||||
|
Wir wollen eine Figur auf dem Papier maßstabsgetreu vergrößern oder verkleinern, z.B. weil der Plan eines Werkstückes – etwa das Gehäuse eines MP3-Players – in einer leicht vergrößerten Version benötigt wird.
Kein Problem, wirst du sagen: Einfach alle Strecken um das x-fache verlängern. Dazu muss man alle Strecken einzeln messen, mit dem Vergrößerungsfaktor multiplizieren und dann neu zeichnen. |
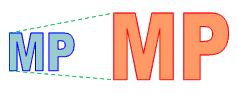
Statt die einzelnen Strecken neu zu berechnen, wird der neue Abstand der Eckpunkte zu einem Zentrum berechnet. Das ist weniger Arbeit.
|
|||||||||||||||||||||||||||||||
|
Im Prinzip geschieht das auch bei der zentrischen Streckung. Allerdings wesentlich effektiver:
Statt alle Strecken und Abstände einzeln neu zu berechnen, berechnet man lieber die neue Position der Eckpunkte, wo sich die Strecken treffen. Das ist normalerweise sehr viel weniger Arbeit. Hierzu geht man von einem vorgegebenen Punkt, dem "Streckungszentrum" Z aus, misst den Abstand der ursprünglichen Punkte zu Z, multipliziert mit dem Vergrößerungsfaktor – er heißt nun "Streckungsfaktor" – und zeichnet die Punkte im neuen Abstand ein. |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| So funktioniert die zentrische Streckung | ||||||||||||||||||||||||||||||||
|
Du gehst von einer Original-Figur aus. Man sagt dir, von welchem Punkt Z aus die Streckung erfolgen soll und man gibt dir den Streckungsfaktor k an.
Nun misst du für jeden Eckpunkt der Figur den Abstand zu Z, multiplizierst ihn mit k und zeichnest den neuen Punkt (den Bildpunkt) in der gleichen Richtung, aber mit diesem neuen Abstand zu Z ein. |
|
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Beispiele | ||||||||||||||||||||||||||||||||
|
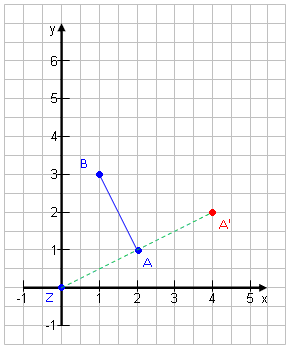
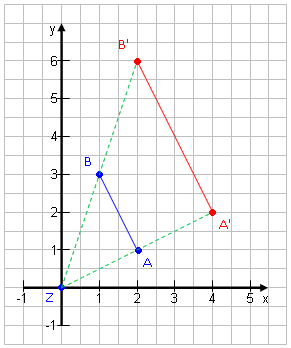
Beispiel 1:
Wir starten mit minimalem Aufwand: Wir strecken die Strecke AB mit A(2|1)und B(1|3) von dem Punkt Z(0|0) aus um den Faktor k = 2. (Wir verdoppeln die Länge.)· Miss den Abstand von A zum Zentrum Z: 2,2 cm · Multipliziere mit k: 2,2 · 2 = 4,4 cm · Zeichne A' im Abstand von 4,4 cm von Z ein. · Miss den Abstand von B zum Zentrum Z: 3,2 cm · Multipliziere mit k: 3,2 · 2 = 6,4 cm · Zeichne B' im Abstand von 6,4 cm von Z ein. · Verbinde die beiden Punkte. |

|
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Beispiele | ||||||||||||||||||||||||||||||||
|
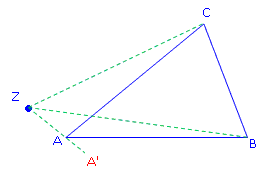
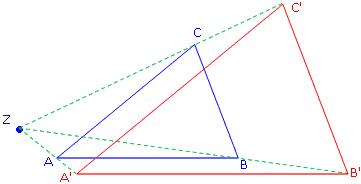
Beispiel 2:
Strecke das Dreieck ABC am Zentrum Z um den Faktor k = 1,5. (Zeichne das Dreieck einfach so gut es geht auf ein Blatt Papier.) · Wir messen wieder den Abstand von A zu Z. · Multiplizieren ihn mit 1,5. · Zeichnen A' im berechneten Abstand ein. · Wir messen den Abstand von B zu Z. · Multiplizieren ihn mit 1,5. · Und zeichnen B' im berechneten Abstand ein. · Das Gleiche mit C. · Und verbinden schließlich alle drei Punkte. |

|
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Ein paar Tricks | ||||||||||||||||||||||||||||||||
|
Folgende Tricks solltest du dir merken:
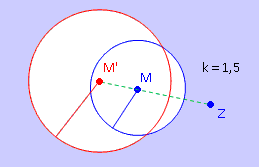
→ Für k > 1 ergibt sich eine Vergrößerung. → Für k < 1 ergibt sich eine Verkleinerung. Ist ja logisch: Wenn du ursprünglich einen Abstand von 3 cm misst und ihn z.B. mit einem Streckungsfaktor von 0,5 multiplizierst, werden daraus nur noch 1,5 cm. Also näher am Zentrum dran. Also Verkleinerung! → Für negative k zeichnet man von Z aus in die entgegengesetzte Richtung. Dämlich, ist aber halt so! → Kreise vergrößert oder verkleinert man, indem man ihren Mittelpunkt zentrisch streckt und anschließend auch den Radius mit k multipliziert. |
|
|||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Die Eigenschaften der zentrischen Streckung | ||||||||||||||||||||||||||||||||
|
Die folgenden Eigenschaften sind eigentlich selbstverständlich:
· Geraden bleiben Geraden. · Kreise bleiben Kreise. · Winkel bleiben in ihrer Größe bestehen |
|
|||||||||||||||||||||||||||||||
|
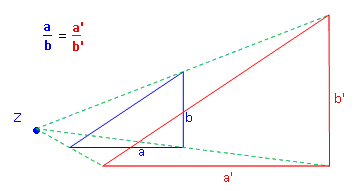
Nun eine Eigenschaft, die nicht mehr selbstverständlich ist, aber absolut entscheidend für den Vierstreckensatz (Strahlensatz) der nächsten Lektion:
· Das Verhältnis zweier Seiten zueinander bleibt gleich. Gemeint ist: Ist in der Originalfigur eine Seite z.B. dreimal so lang wie eine andere, dann ist sie auch in der Bildfigur dreimal so lang. Ist sie im Original 1,4 mal so lang wie eine andere, dann ist sie auch später 1,4 mal so lang etc. Ist aber auch kein Wunder, denn beim Strecken werden ja einfach alle Längen mit dem gleichen Faktor k multipliziert. |
||||||||||||||||||||||||||||||||
|
· Alle Strecken verändern ihre Länge um den Faktor k.
|
||||||||||||||||||||||||||||||||
|
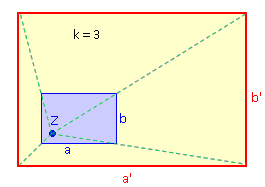
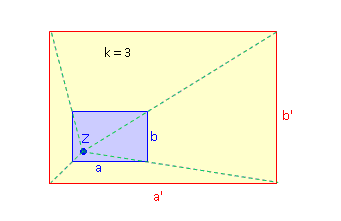
· Der Flächeninhalt verändert sich um den Faktor k2:
A' = k2 · A Hat also beispielsweise eine Figur einen Flächeninhalt A von 10 cm2 und wir um den Faktor k = 2 gestreckt, dann besitzt die Bildfigur anschließend einen Flächeninhalt von A' = 4 · 10 cm2 = 40 cm2. Beispiel rechts: k = 3 A = 1,3 cm · 2 cm = 2,6 cm2 A' = 3,9 cm · 6 cm = 23,4 cm2 damit ist A' = 32 · A |
||||||||||||||||||||||||||||||||