|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||||||||||||
|
Lineare Funktionen sind die einfachste Form der Funktionen. Bei ihnen kommt die Variable x in linearer Form vor, also als normales x.
Käme es als x2 vor, hätte man es mit quadratischen Funktionen zu tun, bei x3 mit kubischen. |
 |
|||||||||||||||||||||||||||||||||||||
|
Lineare Funktionen haben allgemein die Form y = m·x + t. Eine besonders einfache Untergruppe bilden die Funktionen, bei denen das t = 0 ist, also wegfällt. Solche Funktionen, y = m·x, erhält man, wenn es um direkte Proportionalitäten geht, wenn also eine Verdopplung/Verdreifachung der einen Größe auch eine Verdopplung/Verdreifachung der anderen Größe nach sich zieht. (Einkaufspreise, Handy-Tarife, Handwerkerkosten etc.)
|
||||||||||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
| Beispiele für lineare Funktionen | ||||||||||||||||||||||||||||||||||||||
|
Lineare Funktionen haben allgemein die Form y = m·x + t. Dabei sind m und t beliebige Zahlen.
Beispiele: y = 3x + 4 ; y = -0,5x + 1 ; y =
Fällt das t weg, hat man es mit einer besonders einfachen Form zu tun: y = m·x Beispiele: y = 4x ; y = 0,6x ; y =
|
Lineare Funktionen:

|
|||||||||||||||||||||||||||||||||||||
|
Wozu braucht man überhaupt Funktionen?
Funktionen sind Formeln, in die man eine Größe einsetzt, um eine andere zu berechnen. Du setzt zum Beispiel die Anzahl der telefonierten Minuten ein und erhältst den Preis, den du am Ende des Monats zahlen musst. |
||||||||||||||||||||||||||||||||||||||
|
Beispiel:
Bei einem Handytarif ohne Grundgebühr sollen sich die Kosten durch Kosten = 0,40 € mal Anzahl der Minuten berechnen. Nehmen wir für die Minuten die Variable x und für die Kosten, die herauskommt, y, ergibt sich die Funktion: y = 0,4·x |
||||||||||||||||||||||||||||||||||||||
|
Das ist ein sehr einfaches Beispiel, das jeder berechnen kann, auch wenn er nichts von Funktionen versteht. Geht es aber um wichtige Berechnungen im technischen Bereich, im Finanzsektor oder in der Klimaforschung, braucht man sehr wohl dieses Wissen das wir uns hier ganz langsam an den einfachsten Funktionen aneignen.
|
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
| Wertetabelle und Graph | ||||||||||||||||||||||||||||||||||||||
|
Um sich anzusehen, wie schnell die berechnete Größe (z.B. die Kosten) in Abhängigkeit von der eingesetzten Größe (den Minuten) ansteigt oder fällt, erstellt man eine Wertetabelle und trägt die Werte in ein Koordinatensystem ein.
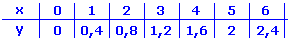
|
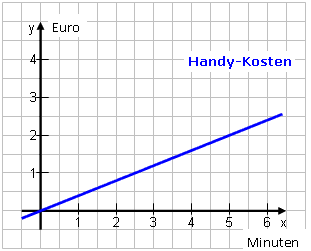
Die Werte steigen immer um den gleichen Betrag an.
Lineare Funktionen ergeben immer Geraden.
Funktionen y = m·x ergeben Ursprungsgeraden. |
|||||||||||||||||||||||||||||||||||||
|
An der Wertetabelle erkennt man, dass der Wert der berechneten Größe Schritt für Schritt immer um den gleichen Betrag ansteigt.
Dies ist immer so bei linearen Funktionen. Jede Minute kostet 40 Cent, also wird es mit jeder Minute 40 Cent teurer. |
||||||||||||||||||||||||||||||||||||||
|
Der Graph ist daher eine Gerade.
Lineare Funktionen ergeben immer Geraden! Die Geraden der besonders einfachen Funktionen y = m·x verlaufen außerdem immer durch den Ursprung. Geraden der allgemeineren Form y = m·x + t verlaufen nicht durch den Ursprung, wie wir später sehen werden. |
||||||||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||||||||
| Die Steigung m | ||||||||||||||||||||||||||||||||||||||
|
Das einzig Interessante an den Funktionen y = m·x ist die Steigung m. Die Zahl, mit der x multipliziert wird. Von ihr hängt es ab, wie schnell die Werte wachsen oder fallen.
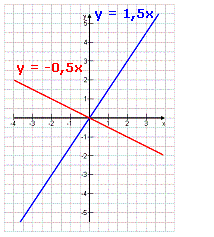
Für m > 0, z.B. y = 1,5x kommen ja mit jedem Schritt 1,5 hinzu, also steigt die Gerade (Handy-Tarif, Kosten für x Flaschen Cola etc. Für m < 0, z.B. y = -0,5x werden in jedem Schritt 0,5 abgezogen, also fällt die Gerade (Verbleibendes Guthaben bei Prepaid-Karten, fallender Wasserstand nach Hochwasser). Für m = 0 erhält man eine Waagerechte, die auf der x-Achse liegt. |
  |
|||||||||||||||||||||||||||||||||||||
|
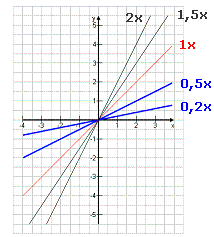
Für m = 1 erhält man die Winkelhalbierende.
Kleinere m, z.B. y = 0,2x y = 0,5x y = 0,8x, ergeben flachere Geraden. Größere m, z.B y = 1,5x y = 2x y = 3,5x ergeben steilere Geraden. |
||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
| Das Steigungsdreieck | ||||||||||||||||||||||||||||||||||||||
|
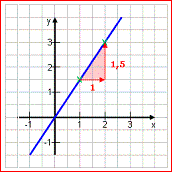
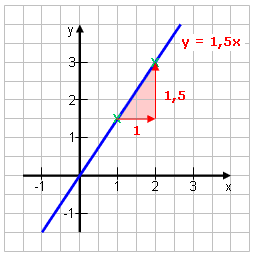
Die Steigung besagt, um wie viel die Gerade steigt oder fällt, wenn man x um 1 erhöht.
m = 2 bedeutet also: Geht man 1 nach rechts, steigt die Gerade um 2. m = -0,5 bedeutet: Geht man 1 nach rechts, fällt die Gerade um 0,5. Man sieht die Bedeutung der Steigung gut am Steigungsdreieck: Um von einem beliebigen Punkt der Geraden zum nächsten zu kommen, geht man 1 nach rechts und die entsprechende Zahl nach oben oder unten. |
|
|||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||
| Die Steigung zeichnen | ||||||||||||||||||||||||||||||||||||||
|
Man kann eine Gerade auf verschiedene Arten zeichnen:
Entweder mit Hilfe einer Wertetabelle. Oder mit Hilfe zweier Punkte. Denn da die Gerade immer die gleiche Steigung besitzt, genügen zwei Punkte, Berechne also die y-Werte für zwei x-Werte und du hast die Gerade. |
Steigung:
1 nach rechts, m nach oben/unten.


|
|||||||||||||||||||||||||||||||||||||
|
Oder direkt über die Steigung:
Du beginnst mit dem Ursprung (0|0). Dann gehst du 1 nach rechts und die Steigung nach oben oder unten. Beispiele: y = 2x → (0|0) , 1 nach rechts, 2 nach oben y = -3x → (0|0) , 1 nach rechts, 3 nach unten |
||||||||||||||||||||||||||||||||||||||
|
Ein Bruch als Steigung
Du startest wieder bei (0|0). Nun gehst du nicht 1 nach rechts, sondern: Den Nenner nach rechts, den Zähler nach oben oder unten. Beispiele: y =
y =
|
||||||||||||||||||||||||||||||||||||||
|
Eine Dezimalzahl als Steigung
Du wandelst die Dezimalzahl in einen Bruch um (in Zehntel), gehst zehn Kästchen nach rechts und die entsprechende Anzahl nach oben oder unten. Beispiele: y = 0,7x → (0|0) , 10 nach rechts, 7 nach oben y = -1,3x → (0|0) , 10 nach rechts, 13 nach unten |
||||||||||||||||||||||||||||||||||||||