|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||
|
Wir suchen nach weiteren Formeln für die Länge von bestimmten Strecken.
In unserem Einstiegskapitel lagen die Punkte, die die Strecke bildeten, immer senkrecht übereinander. Dies ist der einfachste und auch der am häufigsten vorkommende Fall. Wie sieht es nun aus, wenn die Punkte waagerecht nebeneinander liegen oder schräg zueinander? |
 |
|||||||||||||||||||||||||

|
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
| Die Länge einer festen Strecke berechnen | ||||||||||||||||||||||||||
|
Bevor wir versuchen, Formeln zu erstellen, sehen wir uns an, wie man die Länge einer Strecke mit festen Punkten berechnet.
|
|
|||||||||||||||||||||||||
|
Zur Erinnerung:
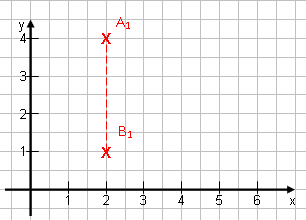
Punkte senkrecht übereinander: Angenommen, der Punkt A1 läge auf einer Höhe von y = 4, der Punkt B1 auf einer Höhe von y = 1. Wie groß ist der Abstand? 3! A1B1 = 4 – 1 = 3Methode: Oberer Punkt minus unterer Punkt. |
||||||||||||||||||||||||||
|
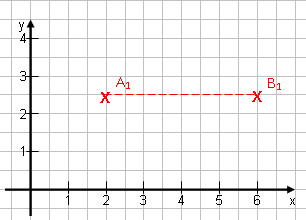
Punkte waagerecht nebeneinander:
Der Punkt A1 läge bei x = 2 und der Punkt B1 bei x = 6. Wie groß ist ihr Abstand? Dies ist genauso einfach, wie wenn die Punkte übereinander lägen: A1B1 = 6 – 2 = 4Methode: Rechter Punkt minus linker Punkt. |
||||||||||||||||||||||||||
|
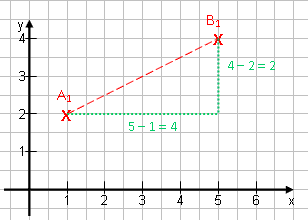
Punkte schräg nebeneinander / Vektoren:
Dies ist der schwierigste Fall. Hier muss man über Pythagoras die Länge der schräg liegenden Strecke berechnen. A(1|2) ; B(5|4) Waagerechter Abstand: 5 – 1 = 4 Senkrechter Abstand: 4 – 2 = 2 Streckenlänge:
|
||||||||||||||||||||||||||
|
Genauso geht man auch vor, wenn man die Länge eines Vektors berechnen möchte:
Länge:
|
||||||||||||||||||||||||||
|
Zusammenfassung:
|
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
| Formeln für senkrechte Strecken | ||||||||||||||||||||||||||
|
Wie man Formeln für die Länge von senkrechten Strecken erstellt, haben wir bereits gesehen. Wir wiederholen es hier trotzdem noch einmal, um uns bei den anderen Strecken leichter zu tun.
|
Formeln erstellen:
Funktionen einsetzen statt Zahlen. 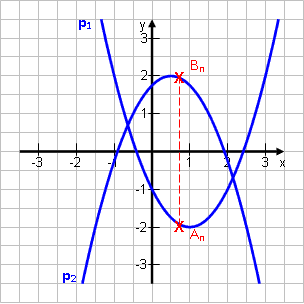
|
|||||||||||||||||||||||||
|
Gegeben seien die Parabeln
p1: y = x2 – 2x – 1 und p2: y = -x2 + x + 1,75. An ϵ p1 ; Bn ϵ p2 ; An und Bn haben die gleiche Abszisse x. Berechne den Abstand AnBn in Abhängigkeit von x im Bereich [-0,64 ; 2,14].
|
||||||||||||||||||||||||||
|
Methode: Oben minus Unten:
(Im angegebenen Intervall liegt p2 oben.) AnBn (x) = -x2 + x + 1,75 – (x2 – 2x – 1)= -2x2 + 3x + 2,75 |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Formeln für waagerechte Strecken | ||||||||||||||||||||||||||
|
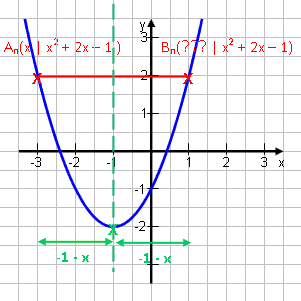
Gegeben sei die Parabel p: y = x2 + 2x – 1
An und Bn liegen beide auf der Parabel p und auf gleicher Höhe y. Berechne den Abstand AnBn in Abhängigkeit von x.Da beide Punkte waagerecht nebeneinander liegen, erhalten wir die Streckenlänge über die Methode: Rechter Punkt minus linker Punkt. |
Waagerechte Strecken kommen am häufigsten in fester Form vor, etwa als Vektor (siehe oben). Als Formel tauchen sie eher selten auf.
|
|||||||||||||||||||||||||
|
Der linke Punk, An liegt bei x.
Der rechte Punkt liegt, wie bereits im letzten Kapitel besprochen, im gleichen Abstand zum Scheitelunkt auf dem anderen Ast der Parabel. Scheitelpunkt: xS =
Abstand von An zum Scheitelpunkt: AnS (x) = -1 – x (rechts minus links)Der Abstand zwischen An und Bn ist doppelt so groß: AnBn (x) = 2·(-1 – x) = -2x – 2 Fertig! |
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
| Formeln für schräg liegende Strecken | ||||||||||||||||||||||||||
| Beispiel 1: | ||||||||||||||||||||||||||
|
Bn verschoben und auf der gleichen Funktion
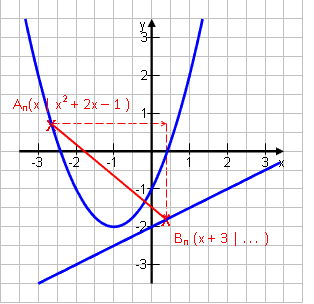
Gegeben: An, Bn ϵ p mit p: y = x2 + 2x – 1 Bn liegt ebenfalls auf p und sei gegenüber An um 3 nach rechts verschoben. Berechne den Abstand AnBn in Abhängigkeit von x.
|
 
Formeln erstellen:
Funktionen einsetzen statt Zahlen. |
|||||||||||||||||||||||||
|
Da die Punkte schräg liegen, brauchen wir die x-Komponenten und die y-Komponenten der beiden Punkte und berechnen dann über Pythagoras die Länge der Strecke.
Wie man die Komponenten bestimmt, haben wir im letzten Kapitel ausführlich gesehen. Deshalb hier nur eine kurze Rechnung und das Ergebnis: An (x | x2 + 2x – 1) Bn (x + 3 | ???) Für Bn den neuen x-Wert in die Parabel einsetzen: yB = (x + 3)2 + 2(x + 3) – 1 = x2 + 6x + 9 + 2x + 6 – 1 = x2 + 8x + 14 An (x | x2 + 2x – 1) Bn (x + 3 | x2 + 8x + 14) |
||||||||||||||||||||||||||
|
Streckenlänge über Pythagoras:
Waagerechter Abstand: 3 (Bn einfach 3 weiter rechts) Senkrechter Abstand: yA – yB = x2 + 2x – 1 – (x2 + 8x + 14) = -6x – 15 Streckenlänge: AnBn 2(x) = 32 + (-6x – 15)2 | √ AnBn (x) = √9 + 36x² + 180x + 225 = √36x² + 180x + 234 |
||||||||||||||||||||||||||
| Beispiel 2: | ||||||||||||||||||||||||||
|
Bn verschoben und auf einer anderen Funktion
An liege wieder auf p mit p: y = x2 + 2x – 1: Bn sei gegenüber An um 3 nach rechts verschoben und liege auf der Geraden g: y = 0,5x – 2. Die Punkte: An (x | x2 + 2x – 1) Bn (x + 3 | ???) yB = 0,5·(x + 3) – 2 = 0,5x + 1,5 – 2 = 0,5x – 0,5 An (x | x2 + 2x – 1) Bn (x + 3 | 0,5x – 0,5) |
|
|||||||||||||||||||||||||
|
Waagerechter Abstand: 3
Senkrechter Abstand: yA – yB = x2 + 2x – 1– (0,5x – 0,5) = x2 + 1,5x – 0,5 Streckenlänge: AnBn 2(x) = 32 + (x2 + 1,5x – 0,5)2 | √ AnBn (x) = √9 + (x² + 1,5x – 0,5)²
|
||||||||||||||||||||||||||
|
Die Funktion unter der Wurzel ist so kompliziert geworden, weil x2 nicht wegfällt. Hätte der Punkt Bn ebenfalls auf einer Parabel gelegen, wäre x2 eventuell wieder weggefallen.
|
||||||||||||||||||||||||||