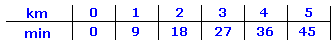Teste dein Wissen
Test 1
Bearbeite die Aufgaben wie gewohnt und kontrolliere dein Ergebnis anhand der Lösung. Anschließend kannst du sie auf einer Prozent-Skala bewerten und deine Note berechnen lassen. Aufgaben, die du nicht bearbeiten möchtest, kannst du mit 'n.w. (nicht werten)' kennzeichnen.
Alles verstanden?
| Welche Bedeutung hat der Proportionalitäts-Faktor? |
|
Lösung
Er gibt an, um wie viel die berechnete Größe steigt, wenn die eingesetzte Größe um 1 zunimmt.
|
|
Note: |
|
|
|
Sind die folgenden Zusammenhänge direkt proportional?
| Ein Handwerker wird zur Reparatur des Badezimmers bestellt. Er berechnet 35 € pro Arbeitsstunde und einmalig 50 € für die Anfahrt. |
|
Lösung
Streng genommen: Nein! Wegen der einmaligen Anfahrt wird die Rechnung nicht doppelt so hoch, wenn er doppelt so lange gearbeitet hat.
Die Kosten für die Arbeitsstunden an sich sind aber direkt proportional zur Arbeitszeit.
|
|
Note: |
|
| Katja lässt einen Stein von einer Brücke in einen Fluss fallen und zählt die Sekunden. Wie tief er wohl nach 1,2,3 ... Sekunden gefallen ist? |
|
Lösung
Nein, nicht direkt proportional! In jeder weiteren Sekunde fällt er zunehmend schneller und damit weiter! Schwer zu berechnen.
|
|
Note: |
|
|
|
Stelle anhand der Wertetabelle fest, ob es sich um eine direkte Proportionalität handelt.
 |
|
Lösung
43 : 1 = 43
90 : 2 = 45
Schon vorbei.
Nein. Die Paare sind nicht quotientengleich.
|
|
Note: |
|
|
|
Berechne den Proportionalitäts-Faktor.
| 300 cm3 eines Metalls wiegen 810 g. (Teile hier Gramm durch cm3.) |
|
Lösung
810 g : 300 cm3 = 2,7 g/cm3
Ein cm3 wiegt 810 g.
|
|
Note: |
|
|
|
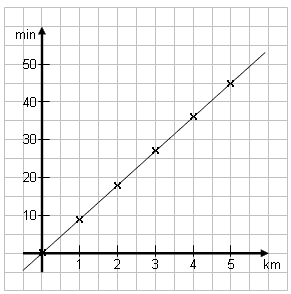
Wertetabelle und Graph.
| Für einen Kilometer braucht ein flotter Fußgänger etwa 9 Minuten. Erstelle Wertetabelle und Graph für 0 bis 5 km. |
|
Lösung
|
|
Note: |
|
|
|