Lektion
   Dreiecke, Rechtecke und Parallelogramme   
Hilfe
Panik-Test
Themenübersicht
zurück zur Lektion
Alles verstanden?
1.1 Wann spricht man von einem spitzwinkligen Dreieck?   Lösung
1.2 Was ist ein Dreieck stumpfwinklig?   Lösung
1.3 Wie bezeichnet man die Seiten eines gleichschenkligen Dreiecks?   Lösung
1.4 In welche Richtung werden Eckpunkte, Seiten und Winkel in der Mathematik benannt?   Lösung
1.5 Wie groß ist die Summe der Winkel im Dreieck?   Lösung
1.6 Wie groß ist die Summe der Winkel im Viereck?   Lösung
1.7 Wie berechnet man den Flächeninhalt eines Rechtecks?   Lösung
1.8 Wie berechnet man den Flächeninhalt eines Parallelogramms?   Lösung
1.9 Wie berechnet man den Flächeninhalt eines Dreiecks?   Lösung
1.10 Wie verläuft eine Höhe in einem Dreieck?   Lösung
1.11 Was ist bei der Flächenberechnung das besondere an einem rechtwinkligen Dreieck?   Lösung
Berechne den Flächeninhalt der folgenden Figuren.
2.1 Dreieck: b = 15 cm; hb = 4 cm   Lösung
2.2 Rechteck: a = 20 cm; b = 6 cm   Lösung
2.3 Parallelogramm: a = 4 cm; b = 5 cm   Lösung
2.4 Parallelogramm: b = 7 cm; hb = 3,5 cm   Lösung
2.5 Dreieck: a = 6 cm; b = 8 cm; c = 5 cm ; hc = 7 cm   Lösung
Berechne die gesuchte Größe
3.1 Dreieck: a = 24 cm; A= 100 cm2; ha = ?   Lösung
3.2 Parallelogramm: A = 68 cm2; hc = 10,5 cm; c = ?   Lösung
3.3 Rechteck: b = 3,2 cm; A = 7,4 cm2; a = ?   Lösung
3.4 Dreieck: A = 10 cm2; a = 5 cm; b = 4,1 cm; c = 2,5 cm; hb = ?   Lösung
3.5 Parallelogramm: a = 7 cm; A = 35 cm2 ; b = ?   Lösung
Nun wird es etwas komplizierter:
4.1 Ein Parallelogramm mit den Seiten a = 10 cm und b = 8 cm besitze die Höhe hb = 4 cm. Wie groß ist die zweite Höhe ha?   Lösung
4.2 Ein Dreieck besitzt die Seiten a = 3 cm, b = 4 cm und c = 3,4 cm. Die Höhe hb beträgt 2,5 cm. Berechne die beiden anderen Höhen.   Lösung
4.3 Ein Parallelogramm mit der Seite a = 17 cm und der Höhe ha = 4,8 cm hat den doppelten Flächeninhalt wie ein gleichschenkliges Dreieck mit der Basis c = 6,8 cm. Wie groß ist die Höhe auf die Basis des Dreiecks?   Lösung
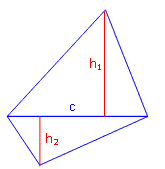
4.4 Zwei Dreiecke besitzen die gleiche Grundseite c = 13 cm, aber unterschiedliche Höhen auf diese Grundseiten. Berechne die Höhe im zweiten Dreieck, wenn die im ersten Dreieck h1 = 7,5 cm beträgt und das erste Dreieck einen dreimal so großen Flächeninhalt besitzt wie das zweite.

   Lösung
Fehler gefunden oder Anregungen?
zurück zur Lektion