| 2.1 |
Ein Kegel besitze die Höhe h = 8 cm und das Volumen V = 200 cm3.
Welchen Umfang hat der Kegel? |
|
Lösung
Als erstes benötigen wir den Radius. V =
· π · r 2 · h 200 =
· π · r 2 · 8 | · 3 : π : 8 23,87 = r 2 | √ r = 4,89 cm u = 2·π·4,89 = 30,72 cm
|
 |
|
| 2.2 |
Zeichne einen Axialschnitt des Kegels. |
|
Lösung
|
 |
|
| 2.3 |
Wie groß ist seine Oberfläche? |
|
Lösung
s = √4,89² + 8² = 9,38 cm
O = π·4,892 + π·4,89·9,38 = 219,22 cm2
|
 |
|
| 2.4 |
Berechne den Winkel α in der Spitze. |
|
Lösung
tan(
) =
= 31,44° | · 2 α = 62,88°
|
 |
|
| 2.5 |
2 cm über der Grundfläche wird der Kegel waagerecht durchschnitten. Wie groß ist die Grundfläche des neuen Kegels?
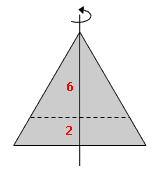 |
|
Lösung
Wir benötigen den Radius r 2 des neuen Kegels. r 2 kann über den Tangens des Winkels in der Spitze berechnet werden. tan 31,44=
| · 6 r 2 = 3,67 cm G = π · r 22 = π · 3,67 2 = 42,31 cm 2
|
 |
|
|




