|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||
|
Um das Rechnen in ebenen Figuren und dreidimensionalen Körpern. Überall in der Industrie, in allen Konstruktions- und Design-Berufen müssen unbekannte Strecken, Flächen und Volumina ermittelt werden.
Mit der Berechnung von Flächeninhalten bei Drei- und Vierecken haben wir vor einigen Lektionen den Anfang gemacht. |
 |
||||||||||||||||||||||||||||
|
Nun geht es weiter mit der Berechnung von Strecken in rechtwinkligen Dreiecken. Der Grund, warum wir uns erst jetzt daran wagen können, ist, dass wir hierzu die Wurzel brauchen und die wurde ja erst in den letzten Kapiteln eingeführt.
In der zehnten Klasse werden wir dann auch Strecken in nicht-rechtwinkligen Dreiecken berechnen. |
|||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Einführung | |||||||||||||||||||||||||||||
|
Das Rechnen in Dreiecken ist deshalb so wichtig, weil du praktisch jede Figur, die gerade, nicht gekrümmte Seiten hat, in Dreiecke unterteilen kannst. Beherrschst du das Dreieck, kommst du mit jeder Figur klar!
Das rechtwinklige Dreieck ist zwar nur ein Spezialfall, aber immerhin einer, der sehr häufig auftritt. Rechte Winkel gibt es massenhaft in ebenen Figuren oder Körpern wie Würfel, Quader, Pyramiden etc. und somit eben auch rechtwinklige Dreiecke. |
Rechtwinklige Dreiecke
kommen in allen möglichen Konstruktionen vor. |
||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Der Satz des Pythagoras | |||||||||||||||||||||||||||||
|
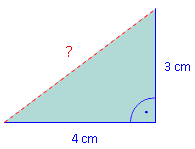
Zeichne doch einmal eine 4 cm lange Seite eines Dreiecks auf ein Blatt Papier. Dann im rechen Winkel dazu eine 3 cm lange Seite.
Wie deutlich zu sehen ist, sind die beiden freien Eckpunkte, die darauf warten, zur dritten Seite verbunden zu werden, festgelegt. Das heißt, die Länge der dritten Seite steht fest! Und alles was nicht flexibel ist, sondern fest steht, lässt sich irgendwie auch berechnen. Miss doch einmal nach, wie lange diese dritte Seite wird. → 5 cm! |

|
||||||||||||||||||||||||||||
|
a = 4 cm ; b = 3 cm → c = 5 cm
Es muss demnach eine Formel geben, die aus den Seitenlängen 3 cm und 4 cm eine dritte Länge zu 5 cm errechnet. Diese Formel ist der Satz des Pythagoras: a2 + b2 = c2 Die wohl bekannteste Formel der Mathematik. Aber: Sie gilt wirklich nur, wenn das Dreieck rechtwinklig ist. Hier: 32 + 42 = 52 9 + 16 = 25 |
|||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||
| Mit Pythagoras eine fehlende Seite berechnen | |||||||||||||||||||||||||||||
|
Mit Hilfe von Pythagoras kann man in einem rechtwinkligen Dreieck aus zwei gegebenen Seiten die dritte, fehlende Seite berechnen.
|
Pythagoras umstellen:
c2 = a2 + b2 a2 = c2 – b2 b2 = c2 – a2 |
||||||||||||||||||||||||||||
|
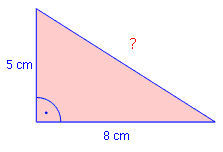
Beispiel 1:
Ein rechtwinkliges Dreieck besitze die Katheten (kurze Seiten) a = 5 cm und b = 8 cm. Wie groß ist seine Hypotenuse (lange Seite)? Lösung: 52 + 82 = c2 25 + 64 = c2 89 = c2 | √ c = 9,43 cm |
|||||||||||||||||||||||||||||
|
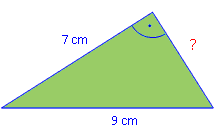
Beispiel 2:
Im nebenstehenden Dreieck soll die fehlende Seite berechnet werden. Vorsicht: Hier soll eine der kürzeren Seiten berechnet werden. Dazu muss man die Formel umstellen. Ursprünglich – mit Plus – formuliert, steht immer die lange Seite (c2) alleine. a2 + b2 = c2 | – b2 a2 = c2 – b2 a2 = 92 – 72 a2 = 32 | √ a = 5,66 cm |
|||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||
| Pythagoras richtig anwenden | |||||||||||||||||||||||||||||
|
Pythagoras ist wirklich eine einfache Formel. Dennoch haben Schüler immer wieder Probleme, sie richtig anzuwenden. Sie klammern sich an die Formulierung mit a, b und c und steigen aus, wenn die Seiten anders heißen.
Deshalb hier ein paar Varianten, die den Blick für das richtige Aufstellen der Formel schärfen sollen. |
Pythagoras verstehen:
lang2 = kurz2 + kurz2 kurz2 = lang2 – kurz2 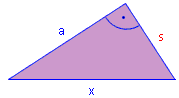
|
||||||||||||||||||||||||||||
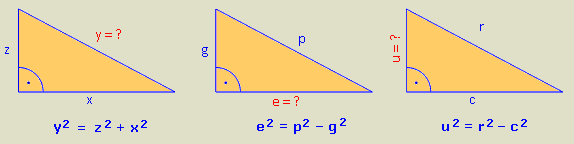
|
|||||||||||||||||||||||||||||
|
Beispiel 3:
Im nebenstehenden Dreieck gilt: a = 5 m ; x = 9 m Berechne die fehlende Seite s. s2 = x2 – a2 s2 = 92 – 52 s2 = 56 | √ s = 7,48 m |
|||||||||||||||||||||||||||||