|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Mit einer einzelnen Gleichung kann man immer nur eine Sache ausrechnen! Wenn die Gleichung x und y enthält, etwa y = 3·x + 4,5 , kann ich entweder eine Zahl für x einsetzen und bekomme y heraus, oder umgekehrt: ich gebe y vor und berechne dann x.
Mit einer Gleichung kann man immer nur eine Variable ausrechnen! Stehe ich vor dem Problem, zwei Variablen berechnen zu müssen, brauche ich dazu zwei Gleichungen. |
 |
||||||||||||||||||||||||||||||
|
Man spricht dann von einem "System mit zwei Gleichungen". Bei drei Variablen bräuchte man drei Gleichungen usw. Ein "lineares Gleichungssystem" ist ein System von Gleichungen, bei dem nur normale x und keine x2 vorkommen.
Wie muss man nun vorgehen, um die beiden Variablen heraus zu bekommen? Dazu gibt es mehrere Wege. Der erste ist ein grafischer. Man löst das Problem also durch Zeichnen. |
|||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Wozu braucht man lineare Gleichungssysteme? | |||||||||||||||||||||||||||||||
|
Du kennst inzwischen lineare Gleichungen. Mit ihnen rechnet man beispielsweise aus, welche Handykosten am Monatsende nach x Minuten Sprechzeit entstehen:
y = 0,25·x + 5,00. Setzt man eine Zahl für x ein (z.B. 150 Minuten), kommt y raus. Oder rückwärts: Gibt man die Kosten für y vor (z.B. 20 €), kann man die Gleichung nach x auflösen und erhält so die Minuten, die man dafür telefonieren kann. y = 0,25·150 + 5,00 (Kosten für 150 Minuten) 20,00 = 0,25·x + 5,00 (Minuten für 20,00 Euro) Wie man sieht, kann man immer nur eine Variable aus einer Gleichung berechnen. |
Mit einer Gleichung
kann man immer nur eine Variable berechnen. 
|
||||||||||||||||||||||||||||||
|
Es gibt aber auch Probleme, bei denen man keine Zahlen hat, die man in die Gleichung einsetzen kann, so dass beide Variablen bestehen bleiben.
Etwa: Zur Verfügung stehen zwei Handytarife: y = 0,5·x + 5,00 und y = 0,1·x + 10,00 Bei welcher Minutenzahl wird der zweite Tarif günstiger als der erste? Wir haben zwei Gleichungen, aber kein x und kein y, das wir einsetzen könnten. Über die einzelnen Gleichungen wirst du keine Lösung finden! Das Problem wird gelöst über ein Gleichungssystem mit zwei linearen Gleichungen. Hier wird zunächst gezeigt, wie man es grafisch lösen kann, in den weiteren Lektionen geht es dann darum, wie man rechnerisch vorgeht. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Die grafische Lösung | |||||||||||||||||||||||||||||||
|
Lineare Gleichungen sind, grafisch gesprochen, Geraden. Wenn wir nun einen x- und einen y-Wert suchen, für die zwei lineare Gleichungen gelten sollen, bedeutet das, grafisch gesprochen, dass wir einen (x|y)-Punkt suchen, der auf beiden Geraden liegen soll!
Und das bedeutet nichts anderes als: Wir suchen den Schnittpunkt der beiden Geraden!!! |
Grafische Lösung:
Beide Geraden zeichnen und den Schnittpunkt ablesen! (gähn!) 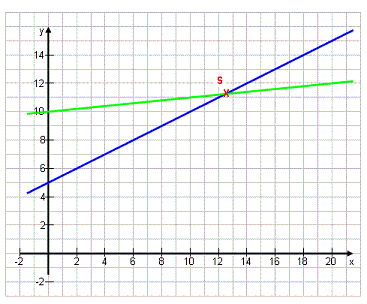
|
||||||||||||||||||||||||||||||
|
Wie man den Schnittpunkt rechnerisch bestimmt, haben wir bereits in einer früheren Lektion gelernt. Hier machen wir zunächst einmal einen kleinen Rückschritt: Statt zu rechnen zeichnen wir. In der nächsten Lektion werden wir dann wieder rechnen.
Der Grund für diese eigentlich dilettantische (dämliche) grafische Methode ist, dass man sehr deutlich sieht, welche Situationen überhaupt auftauchen können. |
|||||||||||||||||||||||||||||||
|
Beispiel:
Gegeben seien die beiden Handy-Tarife: y = 0,5·x + 5,00 und y = 0,1·x + 10,00 (5 € Grundgebühr und 50 Ct pro Minute und 10 € Grundgebühr und 10 Ct/min). Bei welcher Minutenzahl wird der zweite Tarif günstiger als der erste? Wir zeichnen beide Geraden und lesen den Schnittpunkt ab: S(12,5|11,25) Lösung: Ab 12,5 Minuten (bzw. 11,25 €) ist der Tarif mit 10 € Grundgebühr günstiger. |
|||||||||||||||||||||||||||||||

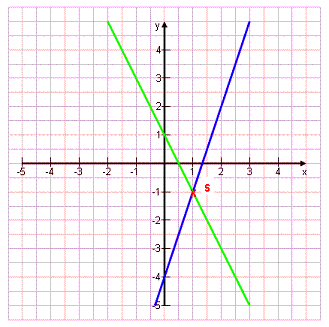
Zweites Beispiel:
Löse das folgende Gleichungssystem grafisch: y = 3x – 4 ˄ y = -2x + 1 Die Geraden zeichnen und den Schnittpunkt ablesen: S(1|-1) Das Zeichen ˄ (und) soll zeigen, dass beide Gleichungen gleichzeitig gelten müssen. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Gleichungen zuerst vorbereiten | |||||||||||||||||||||||||||||||
|
Nicht immer liegen die Gleichungen bereits in der Form vor, wie man sie zum Zeichnen der Geraden braucht, also nach y aufgelöst: y = .....
Aber sehr viel komplizierter macht das die Sache auch nicht. Man formt die beiden Gleichungen getrennt so lange um, bis man sie in die Form y = ... gebracht hat. Dann wird wieder gezeichnet. |
Wie du siehst, beschäftigt sich die Mathematik mit wichtigen und realistischen Fragen des Alltags! :O)
|
||||||||||||||||||||||||||||||
|
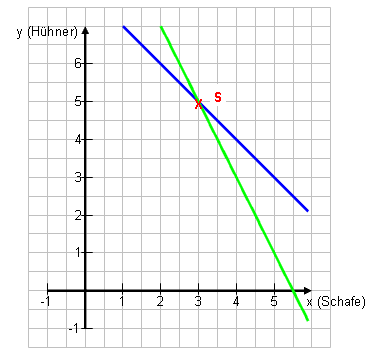
Beispiel
Der Klassiker unter den Gleichungssystemen: Bauer Huber zählt seine Schafe und Hühner: Er zählt insgesamt 8 Köpfe und 22 Füße. Wie viele Schafe und wie viele Hühner besitzt er? Für die Gleichungen setzen wir x für die Anzahl der Schafe und y für die Anzahl der Hühner ein: x + y = 8 (Köpfe) ˄ 4·x + 2·y = 22 (Füße: 4 je Schaf und 2 je Huhn) Erster Schritt: Umformen. x + y = 8 | – x ˄ 4·x + 2·y = 22 | – 4x y = -x + 8 ˄ 2y = -4x + 22 | : 2 y = -x + 8 ˄ y = -2x + 11 Nun liegen beide Gleichungen im Geraden-Stil vor und wir können sie zeichnen und den Schnittpunkt ablesen: S(3|5) Lösung: Der Bauer besitzt 3 Schafe und 5 Hühner. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Nicht alles ist eindeutig lösbar! | |||||||||||||||||||||||||||||||
|
Der eigentliche Grund, warum wir uns überhaupt mit dem grafischen Verfahren beschäftigen, ist der, dass man hier sehr deutlich sieht, welche Situationen auftreten können.
Zwei zusammenhängende Gleichungen zu lösen, bedeutet grafisch gesehen immer, den Schnittpunkt der beiden Geraden zu bestimmen. Dabei kann es zu drei verschiedenen Situationen kommen: |
|
||||||||||||||||||||||||||||||
|
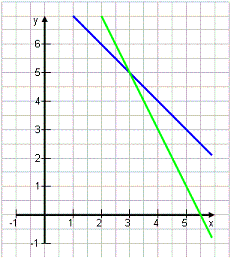
Genau eine Lösung
In aller Regel gibt es einen eindeutigen Schnittpunkt. So wie wir es in den Beispielen oben gesehen haben. Unser Problem, für das wir die Geraden gezeichnet haben, besitzt dann eine eindeutige Lösung. (z.B. "3 Schafe und 5 Hühner.") |
|||||||||||||||||||||||||||||||
|
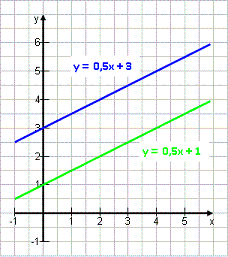
Keine Lösung
Auch dies ist möglich: Unser Problem hat keine Lösung. Grafisch sieht man sofort, wann dies passiert: Wenn beide Geraden parallel verlaufen. Beispiel: Bei welcher Minutenanzahl liefern die beiden Tarife y = 0,5·x + 1 und y = 0,5·x + 3 die gleichen Kosten? Antwort: Nie! Weil der zweite Tarif immer über dem ersten liegt. Er startet höher und steigt gleich schnell an. Die beiden Geraden verlaufen mit der gleichen Steigung, also parallel. |
|||||||||||||||||||||||||||||||
|
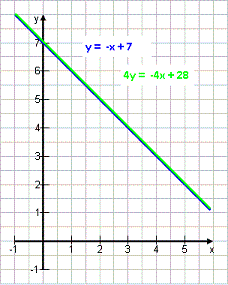
Mehrere oder unendlich viele Lösungen
Es gibt auch Gleichungssysteme, die nicht keine, nicht eine sondern mehrere oder sogar unendlich viele Lösungen haben. Grafisch gesprochen passiert das immer dann, wenn beide Geraden aufeinander liegen. Oder, anders gesagt, wenn es sich bei beiden Geraden um die gleiche Gerade handelt. Beispiel: Bauer Huber hat dieses Mal Schafe und Ziegen. Er zählt 7 Köpfe und 28 Füße: x + y = 7 ˄ 4x + 4y = 28 | : 4 Die zweite Gleichung hilft uns nicht weiter, weil Ziegen genau so viele Füße haben wie Schafe. Teilt man die Gleichung durch 4, kommt eh wieder die erste heraus: x + y = 7 ˄ x + y = 7 Die Aussage stimmt also für 7 Schafe und 0 Ziegen. Oder für 6 Schafe und 1 Ziege für 5 Schafe und 2 Ziegen usw. |
|||||||||||||||||||||||||||||||