|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Hat man die Geradengleichung gefunden, lassen sich allerhand einfache Rechnungen mit ihr durchführen.
Wo schneidet die Gerade die beiden Achsen? In welchem Punkt schneidet sie sich mit einer anderen Geraden? Liegt ein gewisser Punkt auf der Geraden usw. Übrigens werden all diese Rechnungen später bei den Parabeln noch einmal auftauchen. |
 |
||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Fehlende Koordinaten eines Punktes berechnen | |||||||||||||||||||||||||||||||
|
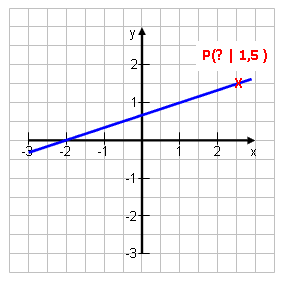
Die Gerade g besitze die Gleichung y = 2x + 5. Die Punkte A(3|y) und B(x|-4) liegen auf der Geraden. Berechne die fehlenden Koordinaten der beiden Punkte.
Nun, die Sache ist denkbar einfach. Erinnerst du dich, wie man mit Punkten umgeht? Richtig: man setzt sie für x und y ein. Die gegebene Koordinate des Punktes setzt man ein, die andere lässt sich dann aus der erstellten Gleichung berechnen. |

|
||||||||||||||||||||||||||||||
|
Die 3 von A(3|y) einsetzen:
y = 2·3 + 5 = 11 → A(3|11) Die y-Koordinate zu berechnen ist simpel: x einsetzen, y ausrechnen, fertig. Die -4 von B(x|-4) einsetzen: -4 = 2x + 5 | – 5 -9 = 2x | : 2 -4,5 = x → B(-4,5|-4) Die x-Koordinate zu berechnen ist kaum schwieriger. Man setzt y ein und löst die Gleichung nach x auf. |
|||||||||||||||||||||||||||||||
|
Zweites Beispiel:
g: y = -0,5x – 3 P(x|-2) Q(1,5|y) Berechne die fehlenden Koordinaten der Punkte. P: -2 = -0,5x – 3 | + 3 1 = -0,5x | :(-0,5) -2 = x → P(-2|-2) Q: y = -0,5·1,5 – 3 = -3,75 → Q(1,5|-3,75) |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Punkte testen | |||||||||||||||||||||||||||||||
|
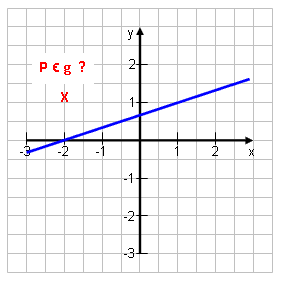
Manchmal soll man testen, ob ein bestimmter Punkt auf der Geraden liegt.
Gegeben sei g: y = 3x – 4 Teste ob P (2|-7) auf g liegt. Super einfach! Die x-Koordinate in die Gleichung einsetzen und nachrechnen, ob wirklich die y-Koordinate des Punktes herauskommt. -7 = 3·2 – 4 ? -7 = 2 falsche Aussage! P liegt nicht auf g. |
Punkte
immer für x und y einsetzen!!! |
||||||||||||||||||||||||||||||
|
Zweites Beispiel:
g: y = -1,5x + 3 P(4|-3) ϵ g ? -3 = -1,5·4 + 3 ? -3 = -3 wahre Aussage! P ϵ g |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Die Achsenschnittpunkte ermitteln | |||||||||||||||||||||||||||||||
|
In welchen Punkten schneidet die Gerade g: y = -2x + 3 die x- und die y-Achse?
Schnittpunkt mit der y-Achse: Hier gibt es nichts zu rechnen, denn die Gerade schneidet die y-Achse natürlich bei t. Hier also bei 3. → Schnittpunkt mit der y-Achse: Sy(0|3) |
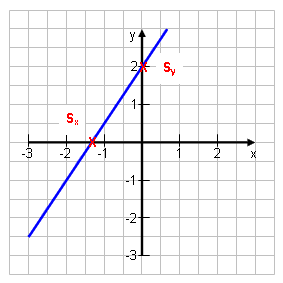

Nullstelle:
Der Wert, bei dem die Gerade durch die x-Achse geht. |
||||||||||||||||||||||||||||||
|
Schnittpunkt mit der x-Achse:
Wenn die Gerade die x-Achse schneidet, ist y = 0! Also können wir y = 0 setzen und die Gleichung nach x auflösen: 0 = -2x + 3 | – 3 -3 = -2x | : (-2) 1,5 = x → Schnittpunkt mit der x-Achse: Sx(1,5|0) Den Wer 1,5, bei dem die Gerade durch die x-Achse geht, nennt man Nullstelle. |
|||||||||||||||||||||||||||||||
|
Zweites Beispiel:
g: y = 0,5x – 2,5 Berechne Sx und Sy. Sy: t = -2,5 → Sy(0|-2,5) Sx: 0 = 0,5x – 2,5 | + 2,5 2,5 = 0,5x | : 0,5 5 = x → Sx(5|0) |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Der Schnittpunkt zweier Geraden | |||||||||||||||||||||||||||||||
|
In welchem Punkt schneiden sich die beiden Geraden g: y = 2x + 1 und h: y = -4x – 2 ?
Wenn sie sich im Punkt P schneiden, bedeutet das, dass der Punkt auf beiden Geraden liegt! Dann ist sein y-Wert, den man mittels der einen Gleichung berechnen kann, aber genau der selbe, den man mit der anderen Gleichung berechnet: 2x + 1 = -4x – 2 Man setzt also die beiden Geradengleichungen gleich!!! Merke dir unbedingt diese Methode: du wirst sie noch 'zig Mal brauchen! Schnittpunkte berechnet man, indem man die beiden Funktionsgleichungen gleich setzt! |
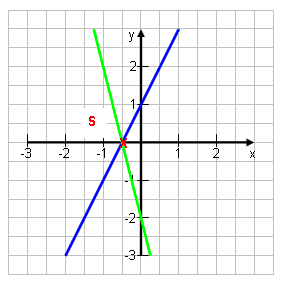 Schnittpunkte berechnen heißt Gleichsetzen!!! |
||||||||||||||||||||||||||||||
|
Aus der entstehenden Gleichung lässt sich leicht der x-Wert berechnen:
2x + 1 = -4x – 2 | + 4x 6x + 1 = -2 | – 1 6x = -3 | : 6 x = -0,5 Der Schnittpunkt hat also einen x-Wert von 0,5. Sein y-Wert lässt sich einfach bestimmen, indem man die -0,5 in eine der beiden Geradengleichungen einsetzt (egal in welche): y = 2·(-0,5) + 1 = 0 → S(-0,5|0) |
|||||||||||||||||||||||||||||||
|
Zweites Beispiel:
Berechne den Schnittpunkt der beiden Geraden m: y = 3x – 2 und n: y = -x + 5 Gleichsetzen: 3x – 2 = -x + 5 | + x 4x – 2 = 5 | + 2 4x = 7 | : 4 x = 1,75 x einsetzen: y = 3·1,75 – 2 = 3,25 → S(1,75|3,25) |
|||||||||||||||||||||||||||||||