|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||
|
Wenn es um das Vereinfachen von Termen geht, steht man immer wieder vor der Situation "Klammer mal Klammer". Und in diesen "Klammer mal Klammer" -Fällen ist es ganz oft der Fall, dass die beiden Klammern gleich sind. Also Klammer mal sich selbst. Oder zumindest fast gleich.
Weil dieser Spezialfall so häufig vorkommt, lernt man das Ergebnis auswendig! So, wie man in Englisch eine Vokabel auswendig lernt oder eine Grammatikregel. |
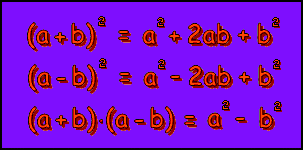 |
||||||||||||||||||||||||

|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Einführung | |||||||||||||||||||||||||
|
Was soll das mit den binomischen Formeln?
Formeln enthalten häufig Terme der Art: (x + 4)2 Im Grunde ist das kein Problem, denn lösen wir das Quadrat auf, kann man einfach "Klammer mal Klammer" rechnen. (x + 4) · (x + 4) |
Woher kommt der seltsame Name?
"Binom" besagt, dass es um zwei Terme geht: Term1 plus Term2 in Klammern zum Quadrat. |
||||||||||||||||||||||||
|
Wenn man solche Spezialfälle, für einige Beispiele ausrechnet, stellt man fest, dass immer wieder das Gleiche passiert:
(x + 4) · (x + 4) = x2 + 4x + 4x + 42 = x2 + 8x + 16 (x + 5) · (x + 5) = x2 + 5x + 5x + 52 = x2 + 10x + 25 (x + y) · (x + y) = x2 + xy + xy + y2 = x2 + 2xy + y2 Erkennst du das Schema in den Ergebnissen? Vorne wird der erste Term quadriert, hinten wird der zweite Term quadriert. Die beiden mittleren Terme sind immer gleich, tauchen also zwei Mal auf und werden zusammengefasst. |
|||||||||||||||||||||||||
|
Genau dieses Schema merkt man sich auswendig!
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Die erste Binomische Formel | |||||||||||||||||||||||||
|
Wir rechnen das Gleiche noch einmal mit a und b durch:
(a + b)2 = (a + b) · (a + b) = a2 + ab + ab + b2 = a2 + 2ab + b2 In Kurzform:
(a + b)2 = a2 + 2ab + b2
|
Viele Schüler
machen den Fehler, den mittleren Term zu vergessen! Null Punkte! ;O( 
12x ergibt sich aus 2 · x · 6. Zwei mal erster Term mal zweiter Term.
Verstehst du den mittleren Term? 2 · x · 3
Warum?
2x zum Quadrat ergibt 4x2 (Alles quadrieren!) Die 9 hinten ist klar. Der mittlere Term: |
||||||||||||||||||||||||
|
(Hans + Rudi)2 = Hans2 + 2 · Hans · Rudi + Rudi2
(Bart + Lisa)2 = Bart2 + 2 · Bart · Lisa + Lisa2 |
|||||||||||||||||||||||||
|
Beispiele:
(x + 6)2 = x2 + 12x + 36 (x + 3)2 = x2 + 6x + 9 (10 + x)2 = 100 + 20x + x2 |
|||||||||||||||||||||||||
|
Etwas unangenehmer wird es, wenn die Terme in der Klammer komplizierter sind:
(2x + 3)2 = 4x2 + 12x + 9 (5x + 2)2 = 25x2 + 20x + 4 (xy + z)2 = x2y2 + 2xyz + z2 (3x + 7y)2 = 9x2 + 42xy + 49y2 |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Die zweite Binomische Formel | |||||||||||||||||||||||||
|
Genauso häufig wie die Situation (... + ...)2 kommt diese hier vor: (... – ...)2. Rechnen wir also ein einziges Mal aus, welches Schema man hier anwenden kann.
(a – b)2 = (a – b) · (a – b) = a2 – ab – ab + b2 = a2 – 2ab + b2 In Kurzform:
(a – b)2 = a2 – 2ab + b2
|
Du musst nur die erste BiFo auswendig lernen. Dann merkst du dir, dass sich die zweite BiFo nur durch ein Minus beim mittleren Term unterscheidet.

2 · x2 · 3xy = 6x3y
|
||||||||||||||||||||||||

(Bart – Lisa)2 = Bart2 – 2 · Bart · Lisa + Lisa2
Bemerkenswert ist, dass das Minus nur beim mittleren Term auftaucht, nicht aber beim dritten Term. Das kommt daher, dass sich beim dritten Term durch Minus mal Minus wieder ein Plus ergibt. |
|||||||||||||||||||||||||
|
Beispiele:
(x – 6)2 = x2 – 12x + 36 (x – 3)2 = x2 – 6x + 9 (10 – x)2 = 100 – 20x + x2 |
|||||||||||||||||||||||||
|
Schwieriger wird es wieder, wenn die Terme in der Klammer etwas komplizierter sind:
(5x – 6)2 = 25x2 – 60x + 36 (7 – 2x)2 = 49 – 28x + 4x2 (2x – 5y)2 = 4x2 – 20xy + 25y2 (x2 – 3xy)2 = x4 – 6x3y + 9x2y2 |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Die dritte Binomische Formel | |||||||||||||||||||||||||
|
Die letzte Binomische Formel ergibt sich, wenn die beiden Klammern fast gleich sind. Nämlich wenn sie die gleichen Terme enthalten, aber einmal mit Plus und einmal mit Minus.
(x + 3) · (x – 3) Dieses Mal gibt es keine abgekürzte Quadrat-Schreibweise. Wir berechnen wieder, welches Rechenschema sich ergibt: (a + b) · (a – b) = a2 – ab + ab – b2 = a2 – b2 In Kurzform:
(a + b) · (a – b) = a2 – b2
|
Die Dritte ist die einfachste!

Die Binomischen Formeln sind Abkürzungen!
In den höheren Klassen musst du Formeln in vielen Schritten umwandeln. Da ist es eine große Erleichterung, wenn man den Fall (... + ...)2 gleich in einem einzigen Schritt erledigen kann. |
||||||||||||||||||||||||

(Bart + Lisa) · (Bart – Lisa) = Bart2 – Lisa2
Überraschender Weise fällt hier der mittlere Term ganz weg. Das rührt daher, dass er einmal mit Plus und einmal mit Minus vorkommt. Und Achtung: Dieses Mal steht ein Minus vor dem letzten Term! |
|||||||||||||||||||||||||
|
Beispiele:
(x + 6) · (x – 6) = x2 – 36 (x + 3) · (x – 3) = x2 – 9 (x + 10) · (x – 10) = x2 – 100 |
|||||||||||||||||||||||||
|
Und zum Schluss wieder mit etwas komplizierteren Termen:
(2x + 4) · (2x – 4) = 4x2 – 16 (5x – 7y) · (5x + 7y) = 25x2 – 49y2 (2x2 + 3xy) · (2x2 – 3xy) = 4x4 – 9x2y2 |
|||||||||||||||||||||||||






