|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||
|
Man kann jede Formel (jeden Term) "vorwärts", aber auch "rückwärts" benutzen: "Vorwärts" heißt: Ich setze eine Zahl für die Variable (meist x) ein und berechne, was dabei herauskommt.
3 · (2x + 5) – 8 x = 2 → 3 · (2·2 + 5) – 8 = 19 "Rückwärts" heißt, ich weiß bereits, was herauskommen soll und interessiere mich dafür, bei welchem x das passiert. 3 · (2x + 5) – 8 3 · (2x + 5) – 8 = 37 x = ??? So ergibt sich eine Gleichung. Und es stellt sich die Frage, wie man systematisch vorgehen kann, um das x herauszukriegen. |
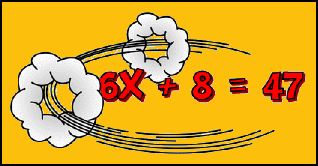
Gleichungen ergeben sich, wenn man bei einer Formel weiß, was herauskommt, und sucht, was man dazu für x einsetzen muss.
|
||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| Einfache Gleichungen lösen | |||||||||||||||||||||||||||||||||||||
|
Eine Gleichung zu lösen heißt, sie so umzuformen, dass man am Ende auf x kommt: x = .....
Dazu muss man auf beiden Seiten die gleiche Umformung durchführen. Genauso, wie wenn ein Händler früher mit einer Waage den Inhalt eines verschlossenen Beutels herausfinden wollte. Er hat auf beiden Seiten die gleiche Anzahl an Münzen weggenommen, hinzugefügt, er hat die Anzahl der Beutel und der Münzen halbiert, verdoppelt etc. Aber immer das Gleiche auf beiden Seiten! |
Immer die gleiche Operation auf beiden Seiten durchführen.
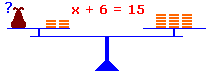
Schau dir diese Lektion aus der 7. Klasse noch einmal an, wenn du die Grundlagen genauer beschrieben haben möchtest.
|
||||||||||||||||||||||||||||||||||||
|
Die vier einfachsten Umformungen
x + 6 = 15 | – 6 x = 9 L = {9} x – 7 = 20 | + 7 x = 27 L = {27} x · 3 = 24 | : 3 x = 8 L = {8} x : 6 = 7 | · 6 x = 42 L = {42} Man löst eine Operation, die mit x verbunden ist immer dadurch auf, dass man die Gegenoperation anwendet: Plus statt Minus, Minus statt Plus. Mal statt Geteilt, Geteilt statt Mal. |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
| Die Reihenfolge der Umformungen | |||||||||||||||||||||||||||||||||||||
|
Besteht die Formel aus mehreren Operationen, stellt sich die Frage, in welcher Reihenfolge man die nötigen Umformungen durchführt.
Die Antwort ist leicht: Zuerst Plus und Minus, dann erst Mal und Geteilt. |
Immer zuerst
Plus und Minus, dann erst Mal und Geteilt!!! 
|
||||||||||||||||||||||||||||||||||||
|
4 · x + 6 = 34
Da in der Formel ja Punkt vor Strich gilt, "haftet" das "Mal" stärker an dem x als das "Plus" oder "Minus". Beim Lösen der Gleichung müssen wir deshalb das "lockerer" gebundene + 6 zuerst weg bekommen. Danach erst das · 4. 4 · x + 6 = 34 | – 6 4 · x = 28 | : 4 x = 7 L = {7} |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| Zuerst vereinfachen, dann umformen | |||||||||||||||||||||||||||||||||||||
|
Gleichungen, die noch unnötig kompliziert sind, werden immer zuerst vereinfacht, dann erst gelöst!
|
Entsteht zum Schluss eine unangenehme Division, kann man sich die Sache erleichtern, indem man einfach einen Bruch hinschreibt. Allerdings sollte der Bruch vollständig gekürzt sein.

|
||||||||||||||||||||||||||||||||||||
|
3x – 6 + x + 13 = 31 + 12 zuerst vereinfachen
4x + 7 = 43 | – 7 dann lösen 4x = 36 | : 4 x = 9 L = {9} |
|||||||||||||||||||||||||||||||||||||
|
8x + 5 – 9 + 13x = 23 – 8 21x – 4 = 15 | + 4 21x = 19 | : 21 x =
|
|||||||||||||||||||||||||||||||||||||
|
3x + 5 – 4x + 8 = 29 -x + 13 = 29 | – 13 -x = 16 | : (-1) x = -16 L = {-16} |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| x-en auf beiden Seiten | |||||||||||||||||||||||||||||||||||||
|
6x – 8 = 4 + 2x
Wie geht man damit um, wenn x nicht nur links sondern auch rechts vorkommt? Kein Problem: Man formt die Gleichung so um, dass es auf einer Seite verschwindet. Man sagt auch: Man bringt alle x auf eine Seite. 6x – 8 = 4 + 2x | – 2x 4x – 8 = 4 Nun kann die Gleichung wie üblich weiter nach x aufgelöst werden. 4x – 8 = 4 | + 8 4x = 12 | : 4 x = 3 L = {3} |
Alle x
auf eine Seite. Alle Zahlen auf die andere Seite.
Es ist egal, ob das x schließlich links oder rechts landet. Du darfst auch gerne die Gleichung jederzeit umdrehen, so dass die linke Seite nach rechts kommt und umgekehrt.
|
||||||||||||||||||||||||||||||||||||

Ein zweites Beispiel: 3x + 7 – 4x + 9 = x + 6 – 5 + 3x -x + 16 = 4x + 1 \| – 4x -5x + 16 = 1 \| - 16 -5x = -15 \| : (-5) x = 3 L = {3} |
|||||||||||||||||||||||||||||||||||||
|
Man könnte auch alle x auf die rechte Seite bringen. Das Ergebnis wäre dasselbe!
3x + 7 – 4x + 9 = x + 6 – 5 + 3x -x + 16 = 4x + 1 | + x 16 = 5x + 1 | – 1 15 = 5x | : 5 3 = x L = {3} |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| Ungewöhnliche Lösungen | |||||||||||||||||||||||||||||||||||||
|
Es gibt zwei Situationen, die zu einer recht ungewöhnlichen Lösung führen.
1. leere Menge 4x + 6 – 4x +1 = 13 (vereinfachen) 7 = 13 L = {} Die x-en sind vollständig weggefallen. Es entsteht eine falsche Aussage. Es gibt keine Zahl, die, für x eingesetzt, 7 gleich 13 werden lässt. Deshalb ist die Lösungsmenge leer. |

|
||||||||||||||||||||||||||||||||||||
|
2. Alle Zahlen
9x – 3 + 2x + 12 – 11x = 9 (vereinfachen) 9 = 9 L = Q Wieder sind alle x-en weggefallen. Es entsteht eine wahre Aussage. 9 = 9. Man darf alle Zahlen einsetzen, 9 ist immer gleich 9. |
|||||||||||||||||||||||||||||||||||||







