
Teste dein Wissen
Test 2
Bearbeite die Aufgaben wie gewohnt und kontrolliere dein Ergebnis anhand der Lösung. Anschließend kannst du sie auf einer Prozent-Skala bewerten und deine Note berechnen lassen. Aufgaben, die du nicht bearbeiten möchtest, kannst du mit 'n.w. (nicht werten)' kennzeichnen.
Alles verstanden?
| Wie heißt ein Dreieck, das einen Winkel von 90° besitzt? |
|
Lösung
|
|
Note: |
|
| Wie zeichnet man den Außenwinkel α1 zu dem Winkel α? |
|
Lösung
Man verlängert am Eckpunkt A eine der beiden Seiten und konstruiert den Nebenwinkel zu α.
|
|
Note: |
|
|
|
Berechne den fehlenden Winkel.
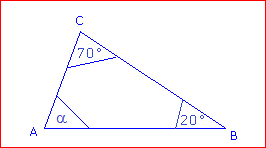 |
|
Lösung
α = 180° – 70° – 20°
= 90°
|
|
Note: |
|
| β = 7° ; γ = 116° ; α = ? |
|
Lösung
α = 180° – 7° – 116°
= 57°
|
|
Note: |
|
|
|
Nun wird's etwas schwieriger
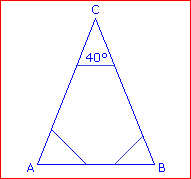
In einem gleichschenkligen Dreieck mit der Basis c ist der Winkel γ = 40° groß. Berechne α und β. |
|
Lösung
180° – 40° = 140°
α = 140° : 2 = 70°
β = α = 70°
|
|
Note: |
|
| In einem rechtwinkligen Dreieck ist γ = 61°. Berechne β. |
|
Lösung
α = 90°
β = 180° – 61° – 90°
= 29°
|
|
Note: |
|
|
|
... und noch etwas schwieriger
| In einem Dreieck ist β = 25°. α ist 4 mal so groß wie γ. Berechne α und γ. |
|
Lösung
180° – 25° = 155°.
α und γ müssen also zusammen 155° groß sein.
Wenn α viermal so groß ist wie γ, sind beide zusammen also fünfmal so groß wie γ.
γ = 155° : 5 = 31°
α = 31° · 4 = 124°
|
|
Note: |
|
|
|
Außenwinkel
| β = 82°. Wie groß ist der Außenwinkel β1? |
|
Lösung
|
|
Note: |
|
|
|






