|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Überall im Bauwesen und im Design muss man Längen und Winkel in allen möglichen Konstruktionen berechnen. Das können Häuser sein oder Bürogebäude, Brücken, Flugzeuge oder Motorräder.
Alle Konstruktionen, außer die runden – sind im Endeffekt aus Dreiecken aufgebaut. Oder Vier- und Fünfecke etc., aber die kann man ja auch wieder in Dreiecke unterteilen. |
 |
||||||||||||||||||||||||||||||
|
Wie man mit Dreiecken rechnet, ist deshalb das wichtigste Thema der Geometrie. In der 8., 9. und 10. Klasse werden wir das alles lernen. Hier beginnt man mit etwas einfachem aber sehr wichtigem: der Winkelsumme.
|
|||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
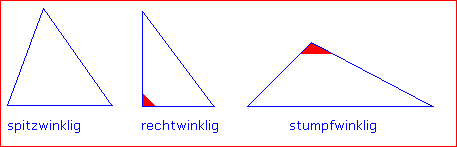
| Wiederholung: Arten von Dreiecken | |||||||||||||||||||||||||||||||
|
Nach Winkel unterscheidet man:
|
|
||||||||||||||||||||||||||||||
|
Nach Seiten unterscheidet man:
|
|||||||||||||||||||||||||||||||
|
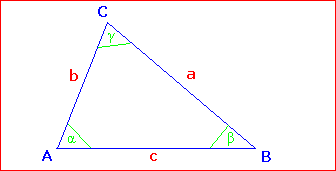
Bezeichnungen im Dreieck: Die Punkte eines Dreiecks bezeichnet man mit Großbuchstaben: A, B und C. Sie sind gegen den Uhrzeigersinn angeordnet. Die Seiten heißen a, b, c und liegen den Punkten gleichen Namens gegenüber. Die Winkel heißen α, β, und γ und liegen bei den Punkten gleichen Namens. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Die Summe der Innenwinkel | |||||||||||||||||||||||||||||||
|
Schau dir dein Geodreieck an.
Wie groß ist der Winkel an der Spitze? Wie groß sind die beiden Winkel unten links und rechts? Antwort: 90° und zwei mal 45°! Alle drei Winkel ergeben also zusammen 180°. Zufall? |

Merke:
Die Summe der Innenwinkel eines Dreieckes ist immer 180° |
||||||||||||||||||||||||||||||
|
Nun zeichne dir ein beliebiges, recht großes Dreieck auf ein Blatt Papier. Messe auch hier alle drei Winkel. Addiere sie.
Ergebnis: Wieder 180° (eventuell kleine Abweichungen wegen Ungenauigkeiten) Dies ist kein Zufall! Egal, wie ein Dreieck aussieht, die Summe seiner (Innen-)Winkel ist immer 180°! |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Anwendung | |||||||||||||||||||||||||||||||
|
Mit dem Wissen, dass die Winkel im Dreieck zusammen 180° ergeben, kann man unbekannte Winkel auszurechnen.
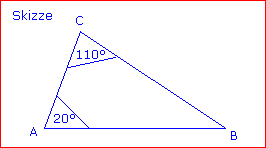
Beispiel 1: In einem Dreieck sind die Winkel α = 20° und γ = 110°. Wie groß ist β? Lösung: Da alles zusammen 180° ergibt, erhält man β, indem man die anderen beiden von 180° abzieht: β = 180° – 20° – 110° = 50°. |
|
||||||||||||||||||||||||||||||
|
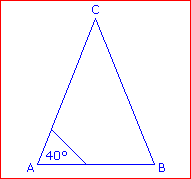
Beispiel 2:
In einem gleichschenkligen Dreieck mit der Basis AB ist der Winkel α = 40°. Berechne die beiden restlichen Winkel. Lösung: gleichschenklig → β = α = 40° γ = 180° – 2 · 40° = 100° |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Die Summe der Außenwinkel | |||||||||||||||||||||||||||||||
|
Die Winkel im Dreieck sind ungeheuer wichtig. Die Winkel außerhalb hingegen nicht so ganz. Trotzdem sei hier erklärt, worum es geht:
Außenwinkel nennt man den Winkel, der sich an einem Eckpunkt außen ergibt, wenn man eine Seite (egal welche) verlängert. α1 ist der Außenwinkel zu α. β1 ist der Außenwinkel zu β etc. |
 
|
||||||||||||||||||||||||||||||
|
Wie man sieht, ergänzen sich ein Innen- und der entsprechende Außenwinkel immer zu 180°.
α + α1 = 180° β + β1 = 180° etc. |
|||||||||||||||||||||||||||||||
|
Wenn man alle Außenwinkel zusammen zählt, ergibt sich eine Summe von 360°:
α1 + β1 + γ1 = 360° Aber, ehrlich gesagt: Man kommt wunderbar ohne dieses Wissen klar! Den Innenwinkel-Satz braucht man absolut! Und man sollte auch wissen, was ein Außenwinkel ist. Und das reicht! |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Die Winkel in Vierecken und anderen n-Ecken | |||||||||||||||||||||||||||||||
|
Wenn man weiß, dass die Winkelsumme im Dreieck 180° ergibt, kann man sich leicht überlegen, wie dies beim Viereck, Fünfeck, etc. ist.
Ein Viereck kann man in zwei Dreiecke unterteilen. Die Winkel addieren sich, also ergeben alle Winkel zusammen 2 · 180° = 360°. |
Merke:
Die Innenwinkel im Viereck ergeben zusammen 360°. 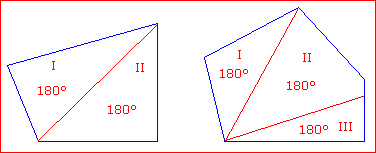
|
||||||||||||||||||||||||||||||
|
Ein Fünfeck kann man in drei Dreiecke unterteilen. Die Winkel addieren sich, also ergeben alle Winkel zusammen 3 · 180°, also 540°.
Ein n-Eck kann man somit in n – 2 Dreiecke unterteilen. Die Winkel addieren sich wieder, also ergeben alle Winkel zusammen (n – 2) · 180°. Viel Spaß beim Rechnen! :O) |
|||||||||||||||||||||||||||||||







