Lektion
   Rechnen mit Vektoren II   
Hilfe
Diskutieren
Panik-Test
Themenübersicht
zu den Übungsaufgaben
Worum geht es?
Es gibt noch zwei Arten von Vektorrechnungen,
die wir noch nicht kennen. Auch sie sind eher
einfach:

Vektoren addieren, wenn man einen Punkt
mehrfach verschiebt.

Und den Mittelpunkt von zwei vorge- 
gebenen Punkten berechnen.
 
In dieser Lektion lernst du
1.Vektoren zu addieren und zu subtrahieren.
2.Wie man den Mittelpunkt einer Strecke findet.
  
Vektoren addieren
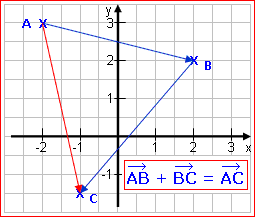
Selbstverständlich ist es nicht verboten, einen Punkt, den man verschoben hat, noch einmal weiter zu verschieben. Und nochmal. Und nochmal ...

Stellt sich die Frage, wo er schließlich ankommt?
 






Vektoren addieren:     

Einfach die Koordinaten addieren.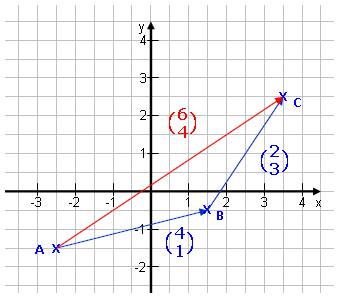



Man könnte immer wieder ausrechnen, wo er zwischendurch landet und dann die nächste Verschiebung dazurechnen. Aber das ist unnötig kompliziert.

Geschickter ist es, einfach alle Verschiebungen, also alle Vektoren, zu addieren! Dadurch erhält man eine einzige Gesamt-Verschiebung. Einen Gesamt-Vektor.
 

Die notwendige Technik ist einfach: Zum Addieren von Vektoren addierst du einfach ihre Koordinaten.
 
Beispiele:

→
AB
 
 =  (
4
1
 ) ; 
→
BC
 
 =  (
2
3
 )
 
Berechne den Gesamt-Vektor 
→
AC
 
.
 

→
AC
 
 =  (
4 + 2
1 + 3
 ) =  (
6
4
 )
 


→
PQ
 
 =  (
3
4
 ) ; 
→
QR
 
 =  (
-5
0
 ) ; 
→
RS
 
 =  (
0
-0,5
 )
 
Berechne den Gesamt-Vektor 
→
PS
 
.
 

→
PS
 
 =  (
3 + (-5) + 0
4 + 0 + (-0,5)
 ) =  (
-2
3,5
 )
  
Vektoren subtrahieren
Manchmal läuft die Sache genau anders herum: Zwei oder mehr Vektoren wurden addiert und man soll aus dem Gesamt-Vektor und einem der ursprünglichen Vektoren den anderen ursprünglichen Vektor berechnen.

Statt die zwei ursprünglichen Vektoren zu addieren, muss man nun natürlich den Gesamt-Vektor minus den einen Teil-Vektor rechnen.
 

erster Vektor:    
→
AB
 
 =  (
3
2
 ) 
 
Gesamt-Vektor: 
→
AC
 
 =  (
10
7
 ) 
 

zweiter Vektor:  
→
BC
 
 =  (
10 – 3
7 – 2
 ) =  (
7
5
 )

  
Der Mittelpunkt einer Strecke
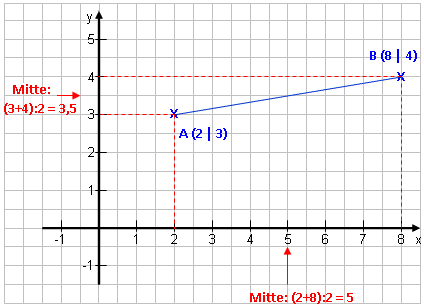
Wenn du zwei Punkte bekommst, kannst du berechnen, wo genau die Mitte dieser beiden Punkte liegt. Wie funktioniert das?

Nehmen wir A (2 | 3) und B (8 | 4). Wo liegt der Mittelpunkt?
 

:long


      
Mittelpunkt:

Die Koordinaten addieren und durch 2 teilen.

x = (xA+xB):2  y = (yA+yB):2







Punkt A liegt bei 2 in x-Richtung, Punkt B liegt bei 8 in x-Richtung. Wo hat also der Mittelpunkt seine x-Koordinate? Naja, eben genau in der Mitte davon.

Wie berechnet man die Mitte zweier Zahlen? Man addiert und teilt durch 2. Genauso wie du den Mittelwert von zwei Noten berechnest.

Hier: xm = (2 + 8) : 2 = 5  Er liegt bei 5.
 
Auf die gleiche Art verfahren wir mit den y-Koordinaten: Punkt A liegt bei 3, Punkt B bei 4. Der Mittelpunkt also genau in der Mitte: 

ym = (3 + 4) : 2 = 3,5

Ergebnis: Die Mitte ist M (5 | 3,5).
 
Beispiele:

P (3 | 8) ; Q (6 | 4)  Berechne den Mittelpunkt.

x = (3 + 6):2 = 4,5 
y = (8 + 4):2 = 6  →  M (4,5 | 6)
 
P (-2 | 6) ; Q (3 | 1)  Berechne den Mittelpunkt.

M:  M ( (-2 + 3):2 | (6 + 1):2 )  =  M (0,5 | 3,5)
 
E (0,5 | -3) ; F (-4 | 10)  Berechne den Mittelpunkt.

M:  M ( (0,5 + (-4)):2 | (-3 + 10):2 ) = M (-2,25 | 3,5)
 

Fehler gefunden oder Anregungen?