|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||
|
Rechtwinklige Dreiecke sind gut und schön, sie tauchen überraschend häufig auf. Aber dennoch handelt es sich bei ihnen nur um einen Spezialfall.
Denn bei weitem nicht alle Dreiecke sind rechtwinklig. Wie aber berechnet man fehlende Seiten, Diagonalen und Winkel in allgemeinen Dreiecken? |
 |
||||||||||||||||||||||||||||||||
|
Hierzu gibt es den Sinussatz und den Kosinussatz. Sie gelten in allen Dreiecken, egal ob rechtwinklig oder nicht. Aber sie sind etwas schwieriger zu handhaben als die einfachen Sinus-, Kosinus- und Tangens-Funktionen.
Die meisten Seiten und Winkel im allgemeinen Dreieck berechnet man mit dem Sinussatz. Mit ihm werden wir beginnen. In zwei Situationen braucht man hingegen den Kosinussatz. Um ihn geht es dann in der nächsten Lektion. |
|||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| Der Sinussatz | |||||||||||||||||||||||||||||||||
|
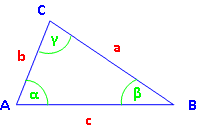
In jedem Dreieck gelten folgende Gleichungen:
|

DREI
Größen du immer brauchst, um in einem Dreieck rechnen zu können! (M. Y.) |
||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
In Worten:
Teilst du die Länge einer Seite durch den Sinus des gegenüber liegenden Winkels, etwa
Der Sinussatz besteht also eigentlich aus drei Gleichungen, von denen man sich immer die passende heraussucht: |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
|
Man rechnet mit einer Gleichung, die vier Größen enthält. Das bedeutet, dass man drei Größen braucht. Dann kann man die vierte Größe berechnen.
Für den Sinussatz braucht man zwei Winkel und eine Seite (und kann dann die andere Seite berechnen) oder zwei Seiten und einen Winkel (und kann dann den gegenüber liegenden Winkel berechnen). Auf jeden Fall geht es immer um Pärchen von Seiten und gegenüber liegenden Winkeln. |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| Seiten berechnen | |||||||||||||||||||||||||||||||||
|
Am einfachsten ist es, mit Hilfe des Sinussatzes Seiten zu berechnen.
→ Stelle den Sinussatz mit den passenden Pärchen auf. → Beginne mit der Seite, die du berechnen möchtest. → Umformung: mit dem linken Nenner malnehmen → ausrechnen |
Sinussatz:
Pärchen von Seiten und gegenüber liegenden Winkeln. 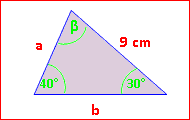
|
||||||||||||||||||||||||||||||||
|
Beispiel:
Berechne im nebenstehenden Dreieck die fehlenden Seiten. a:
a =
Für die Seite b brauchen wir den gegenüber liegenden Winkel β. β = 180° – 30° – 40° = 110° b:
b =
|
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| Winkel berechnen | |||||||||||||||||||||||||||||||||
|
Zum Berechnen von Winkeln geht man ähnlich vor.
→ Stelle den Sinussatz mit den passenden Pärchen auf. → Beginne mit dem Winkel, den du berechnen möchtest. → Umformung: mit dem linken Nenner malnehmen → ausrechnen Dabei stellt man den Sinussatz quasi auf den Kopf, so dass die Winkel nun oben stehen und die Seiten unten. Dadurch werden die Umformungen viel einfacher, denn die gesuchte steht nun wieder oben und nicht unten im Nenner. |
|
||||||||||||||||||||||||||||||||
|
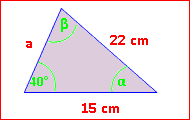
Beispiel:
Berechne im nebenstehenden Dreieck die fehlenden Winkel. Wir müssen mit β beginnen. Denn für α fehlt uns die gegenüber liegende Seite.
Wir stellen den Sinussatz also auf den Kopf und beginnen wieder mit der gesuchten Größe.
sin β =
β = 25,99° α = 180° – 40° – 25,99° = 114,01° |
|||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||
| Winkel sind nicht immer eindeutig | |||||||||||||||||||||||||||||||||
|
Gar nicht so schwer, hast du dir wahrscheinlich bisher gedacht. Doch leider gibt es ein Problem, wenn man Winkel mit dem Sinussatz ausrechnet.
Im vorletzten Rechenschritt, gleich bevor man den Winkel erhält, liefert der Taschenrechner uns den Sinus des Winkels. Zum Beispiel: sin β = 0,5 Daraus erhalten wir β = 30°. Doch leider gibt es noch einen zweiten Winkel, dessen Sinus 0,5 ergibt: β = 150°! Tippe einfach sin 150° in deinen Taschenrechner ein, und du wirst es sehen. Davon sagt uns der Taschenrechner aber nichts, wenn wir den Winkel durch [SHIFT] [sin] 0,5 ermitteln. Er liefert uns lediglich 30°. Dass es einen zweiten Winkel geben kann, müssen wir wissen. |
Beim Sinussatz kann es einen zweiten Winkel geben:
α ˅ 180° – α 
|
||||||||||||||||||||||||||||||||
|
Den zweiten Winkel bekommt man leicht heraus, wenn man 180° minus den ersten rechnet:
β = 30° ˅ β = 180° – 30° = 150° In unserem Beispiel oben hätte es ebenfalls einen zweiten Winkel geben können: β = 25,99° ˅ β = 180° – 25,99° = 154,01° |
|||||||||||||||||||||||||||||||||
|
Welcher Winkel ist nun der richtige?
Die beiden Winkel unterscheiden sich deutlich, da der eine immer kleiner und der andere immer größer als 90° ist. 1. Manchmal kann man an der Skizze der Aufgabenstellung entscheiden, ob der gesuchte Winkel kleiner oder größer als 90° ist. Den zweiten, falschen Winkel streicht man dann durch. 2. Oder du vergleichst die Winkel mit anderen Winkeln und deren gegenüberliegenden Seiten. In unserem Beispiel hätte man argumentieren können: Wir suchen den Winkel gegenüber von b. b ist mit 15 cm kleiner als c mit 22 cm. Also muss auch unser Winkel β kleiner sein als die 40°, die c gegenüber liegen. Deshalb ist 29,99° richtig und 154,01° falsch. In Kürze: β = 25,99° ˅ β = 180° – 25,99° = 154,01° 15 cm < 22 cm → β = 25,99° 3. Manchmal gibt es aber überhaupt keinen Anhaltspunkt, welcher Winkel richtig ist. Dann muss man beide Alternativen stehen lassen. |
|||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||
| Flächeninhalt eines Dreiecks | |||||||||||||||||||||||||||||||||
|
Wir kennen bereits eine Formel zur Berechnung des Flächeninhalts eines Dreiecks:
A =
Da man die Höhe h mit Sinus und einer weiteren Seite berechnen kann, kommt nun eine zweite – einfache – Formel hinzu, die du noch öfters als die erste anwenden wirst: A =
|

|
||||||||||||||||||||||||||||||||
|
Natürlich gilt das gleiche auch an den anderen beiden Ecken des Dreiecks:
A =
Du merkst dir aber nur die erste Formel. Der Rest ist eh klar. |
|||||||||||||||||||||||||||||||||
|
Beispiel:
Berechne den Flächeninhalt eines Dreiecks mit α = 40° ; b = 7 cm ; c = 10 cm. Lsg: A =
|
|||||||||||||||||||||||||||||||||