|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
In allen Berufen und Fachgebieten, in denen etwas konstruiert wird, also im Architektur- oder Ingenieurbüro, in der Landschaftsplanung, in der Fahrzeugkonstruktion oder im Design und vielen, vielen Gebieten mehr, müssen geometrische Berechnungen durchgeführt werden.
Da geht es um Drei-, Vier-, Fünf- und Sechsecke, mal um regelmäßige, mal um unregelmäßige Formen. Aber die Herangehensweise ist praktisch immer die gleiche: Teile deine Figur in Dreiecke und berechne die gesuchten Größen in diesen Dreiecken. |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Deshalb ist das Rechnen im Dreieck von so zentraler Bedeutung. Alles wird in Dreiecke aufgeteilt. Kennst du dich im Dreieck aus, beherrschst du jede Figur.
Wir starten zunächst mit der Dreiecksform, die am häufigsten auftaucht: dem rechtwinkligen Dreieck. Die Funktionen zur Berechnung sind besonders einfach: Sinus, Kosinus und Tangens. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Wiederholung | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
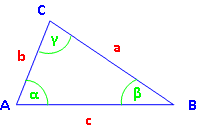
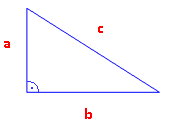
Bezeichnungen im Dreieck:
Eckpunkte A, B, C gegen den Uhrzeigersinn. Seiten a, b, c gegenüber den Eckpunkten. Winkel α, β, γ bei den Eckpunkten. Achtung: im Viereck: Seiten a, b, c, d neben den Punkten! Gleichschenklige Dreiecke: Zwei Seiten gleich lang, zwei Winkel gleich groß. Gleichseitige Dreiecke Drei Seiten gleich lang, alle Winkel 60°. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Winkelsumme
Dreieck: α + β + γ = 180° Viereck: α + β + γ + δ = 360° Flächeninhalt A =
Pythagoras Nur im rechtwinkligen Dreieck: a2 + b2 = c2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Sinus, Kosinus und Tangens im rechtwinkligen Dreieck | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Im rechtwinkligen Dreieck, und wirklich nur im rechtwinkligen Dreieck, gibt es einen einfachen Weg, die Winkel zu berechnen.
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
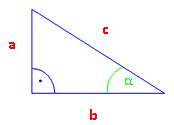
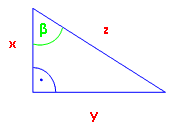
Die Hypotenuse ist immer die längste Seite im rechtwinkligen Dreieck. Welche Seite aber die An- und welche Seite die Gegenkathete ist, hängt davon ab, welchen Winkel man berechnen will.
Für den Winkel α im Dreieck rechts ergibt sich zum Bespiel: sin α =
Für den Winkel β im Dreieck rechts ergibt sich stattdessen: sin β =
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Winkel berechnen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beispiel 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
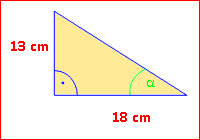
Wir berechnen zuerst α.
Von α aus gesehen, sind die beiden gegebenen Seiten die Gegenkathete und die Hypotenuse. Für dieses Pärchen ist der Sinus verantwortlich. sin α
Nun [SHIFT] [sin] [=] drücken. α = 22,02° β berechnen wir über die Winkelsumme: β = 180° – 90° – 22,02° = 67,98° |
Tasschenrechner richtig eingestellt?
Die Einstellung "Angel" (Winkel) muss auf "Deg" stehen. Oft steht sie auf "Rad" und liefert falsche Ergebnisse. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beispiel 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
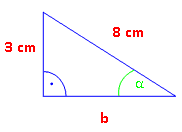
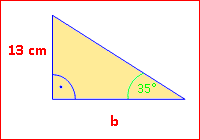
Wir berechnen zuerst β.
Von β aus gesehen, sind Ankathete und Hypotenuse gegeben. Also Kosinus. cos β
Nun [SHIFT] [cos] [=] drücken. β = 44,42° Nun noch α: α = 180° – 90° – 44,42° = 45,58° |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beispiel 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
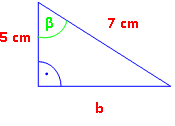
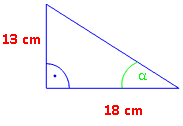
Von α aus gesehen, haben wir es mit den beiden Katheten zu tun. Also Tangens.
tan α
[SHIFT] [tan] → α = 35,84° β= 180° – 90° – 35,84° = 54,16° |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Seiten berechnen | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Mit Sinus, Kosinus und Tangens kann man auch fehlende Seitenlängen eines Dreiecks berechnen. Dazu müssen ein Winkel und eine Seitenlänge gegeben sein.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beispiel 1 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
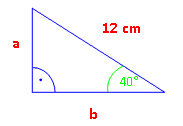
Wir berechnen zuerst a.
Von den 40° aus gesehen geht es um Gegenkathete und Hypotenuse. Also Sinus. sin 40°
a = 12·sin 40° In den Taschenrechner eingeben: 12 · sin 40° a = 7,71 cm b über Pythagoras: (Kosinus oder Tangens gingen auch) b2 = 122 – 7,712 | √ b = 9,20 cm β = 180° – 90° – 40° = 50° |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beispiel 2 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
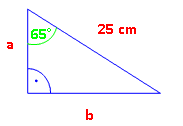
Wir berechnen wieder zuerst a.
Von den 65° aus gesehen geht es um Ankathete und Hypotenuse. Also Kosinus. cos 65°
a = 25· cos 65° in den Taschenrechner eingeben → a = 10,57 cm b über Sinus: (Tangens oder Pythagoras gingen auch) sin 65°
b = 25 · sin 65° b = 22,66 cm β = 180° – 90° – 65° = 25° |
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Beispiel 3 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
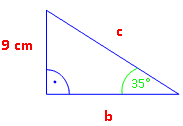
tan 35°
b · tan 35° = 9 | : tan 35° b =
b = 12,85 cm c über Pythagoras: c2 = 92 + 12,852 | √ c = 15,69 cm β = 180° – 90° – 35° = 55° |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Tangens und die Steigung von Geraden | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Etwas unerwartet taucht Tangens auch in einigen Aufgaben auf, die sich im Koordinatensystem abspielen. Dort kann man die Steigung von Geraden über den Tangens des Steigungswinkels ausrechnen.
Die allgemeine Form einer Geraden lautet ja y = m·x + t Dabei ist m die Steigung und t der y-Achsenabschnitt. m können wir bisher nur berechnen, wenn man uns zwei Punkte gibt, z.B. A(2|1) und B(5|7):
|
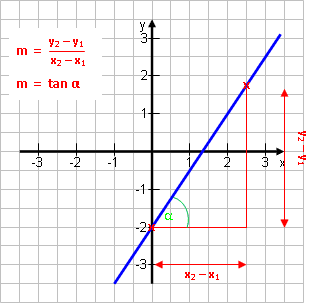
Steigung
einer Geraden m = tan α |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Nun kommt eine zweite Möglichkeit hinzu: Man gibt uns den Steigungswinkel. Das ist der Winkel, den die Gerade mit der Waagerechten einschließt. Für diesen Winkel gilt:
m = tan α |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Beispiel:
Eine Gerade besitzt den Steigungswinkel α = 60° und läuft durch den Punkt P(4|3). Gib ihre Gleichung an. m = tan 60° = 1,73 → y = 1,73·x + t P für y und x einsetzen: 3 = 1,73·4 + t 3 = 6,92 + t | - 6,92 -3,92 = t → y = 1,73·x – 3,92 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||