|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||
|
Das Lösen quadratischer Gleichungen dient nicht nur dazu, herauszufinden, wann eine Funktion einen bestimmten Wert erreicht, also z.B. y = 3, sondern wird vor allem auch zur Berechnung von Schnittpunkten verwendet.
Bei welchem x-Wert schneidet die Funktion die x-Achse? Bei welchem y-Wert schneidet sie die y-Achse? Wo liegt ihr Schnittpunkt mit einer anderen Geraden? Wo liegen die Schnittpunkte mit einer anderen Parabel? |
 |
||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
| Schnittpunkte mit der x-Achse (Nullstellen) | |||||||||||||||||||||||||||||||||||
|
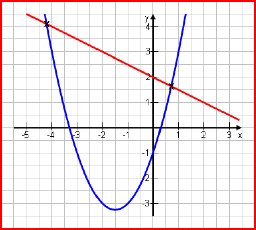
Gegeben: y = x2 + 3x – 1
Wo schneidet die Parabel die x-Achse? Man sagt auch: Wo hat die Parabel ihre Nullstellen? Wie man sich an der Graphik rechts klar machen kann, ist dort, wo eine Funktion die x-Achse schneidet, der y-Wert gleich 0. Die x-Achse selbst liegt eben bei: y = 0 Wir setzen also 0 für y ein: |
Schnittpunkt mit der x-Achse:
0 = ax2 + bx + c D = .... x1/2 = .... |
||||||||||||||||||||||||||||||||||
|
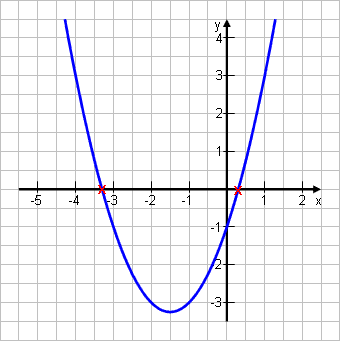
0 = x2 + 3x – 1
Kein Problem! Die Technik, um dies aufzulösen, beherrschen wir inzwischen: D = b2 – 4ac = 32 - 4·1·(-1) = 13 D > 0 → 2 Lösungen x1 =
x2 =
|
|||||||||||||||||||||||||||||||||||
|
Ein Blick auf den Graphen bestätigt uns diese beiden Werte.
Ergebnis: Die Parabel schneidet die x-Achse bei x=0,30 und bei x=-3,30. Oder: Die Schnittpunkte mit der x-Achse liegen bei Sx1(0,30|0) und Sx2(-3,30|0). |
|||||||||||||||||||||||||||||||||||
|
Übrigens:
Hätte unsere Parabel etwas höher gelegen, so dass sie die x-Achse gerade noch berührt, wäre bei unserer Rechnung nur ein Schnittpunkt heraus gekommen. Die Determinante wäre 0 gewesen. D = 0 Hätte die Parabel noch höher gelegen (oder tiefer aber umgedreht), so hätten wir überhaupt keinen Schnittpunkt erhalten, da die Determinante dann negativ gewesen wäre. D < 0 |
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
| Schnittpunkt mit der y-Achse | |||||||||||||||||||||||||||||||||||
|
Gegeben: y = x2 + 3x – 1
Wo schneidet die Parabel die y-Achse? Man sagt auch: Wo hat die Parabel ihren y-Achsenabschnitt? Schau dir noch einmal die Parabel in der Graphik oben an. Siehst du, dass es immer nur einen Schnittpunkt mit der y-Achse geben kann? Und mehr noch: Es muss sogar immer genau einen Schnittpunkt geben. |
Schnittpunkt mit der y-Achse:
x = 0 y = a·02 + b·0 + c = c 
|
||||||||||||||||||||||||||||||||||
|
Dieser Schnittpunkt ist geschenkt! Denn:
Wo die Parabel die y-Achse schneidet, ist x = 0! Wir müssen also nur 0 für x einsetzen und den y-Wert ausrechnen, ohne eine Gleichung zu lösen. x = 0 y = 02 + 3·0 – 1 = -1 fertig! Die Parabel schneidet die y-Achse bei y = -1 bzw. im Punkt Sy(0|-1). |
|||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||
| Parabel schneidet Gerade | |||||||||||||||||||||||||||||||||||
|
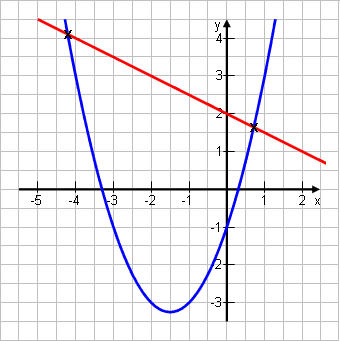
Gegeben seien eine Parabel p: y = x2 + 3x – 1 und eine Gerade g: y = -0,5x + 2. Berechne die beiden Punkte, in denen sich die zwei Funktionen schneiden.
"Schnittpunkt" bedeutet, dass es sich um Punkte handelt, durch die sowohl die eine Funktion wie auch die andere laufen. Dort sind also die beiden Funktionen gleich. |
|
||||||||||||||||||||||||||||||||||
|
Wir setzen daher die beiden Funktionen gleich!
-0,5x + 2 = x2 + 3x – 1 Na, siehst du schon, wo die Sache hin läuft? Wir packen alles auf eine Seite und haben wieder die Voraussetzung dafür geschaffen, die Mitternachtsformel anwenden zu können: -0,5x + 2 = x2 + 3x – 1 | + 0,5x – 2 0 = x2 + 3,5x – 3 |
|||||||||||||||||||||||||||||||||||
|
Mitternachtsformel:
D = b2 – 4ac = 3,52 – 4·1·(-3) = 24,25 D > 0 → 2 Lösungen x1 =
x2 =
Ein Blick nach oben zeigt uns wieder, dass wir richtig liegen. |
|||||||||||||||||||||||||||||||||||
|
Um die Schnittpunkte angeben zu können, brauchen wir aber noch die zugehörigen y-Werte. Dazu setzen wir einfach die x-Werte in eine der Funktionen ein, am besten in die der Geraden:
y1 = -0,5·0,72 + 2 = 1,64 y2 = -0,5·(-4,22) + 2 = 4,11 Ergebnis: Parabel und Gerade schneiden sich in den Punkten S1(0,72|1,64) und S2(-4,22|4,11). |
|||||||||||||||||||||||||||||||||||
|
Auch hier hätte es wieder nur einen oder sogar überhaupt keinen Schnittpunkt geben können, wenn die Gerade die Parabel nur berührt hätte oder an ihr vorbei gelaufen wäre. Dementsprechend wäre die Determinante wieder 0 oder negativ gewesen.
|
|||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||
| Parabel schneidet Parabel | |||||||||||||||||||||||||||||||||||
|
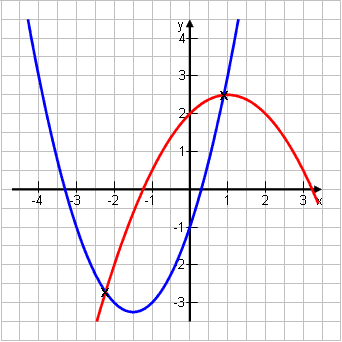
Gegeben seien die Parabeln p1: y = x2 + 3x – 1 und p2: y = -0,5x2 + x + 2. Berechne die Punkte, in denen sich die zwei Funktionen schneiden.
|
|
||||||||||||||||||||||||||||||||||
|
Wieder die gleiche Logik: Wo sich beide Parabeln schneiden, sind sie gleich. Also setzen wir die Funktionen gleich. Danach läuft wieder alles wie gehabt.
Gleichsetzen: -0,5x2 + x + 2 = x2 + 3x – 1 Alles auf eine Seite: -0,5x2 + x + 2 = x2 + 3x – 1 | + 0,5x2 – x – 2 0 = 1,5x2 + 2x – 3 |
|||||||||||||||||||||||||||||||||||
|
Mitternachtsformel:
D = b2 – 4ac = 22 – 4·1,5·(-3) = 22 D > 0 → 2 Lösungen x1 =
x2 =
y-Werte (x1/2 in eine der beiden Funktionen einsetzen): y1 = 0,902 + 3·0,90 – 1 = 2,51 y2 = (-2,23)2 + 3·(-2,23) – 1 = -2,71 Ergebnis: Die Schnittpunkte sind S1(0,90|2,51) und S2(-2,23|-2,71). Auch hier hätte es wieder nur einen oder keinen Schnittpunkt geben können. |
|||||||||||||||||||||||||||||||||||