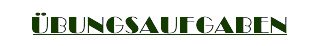|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Wir haben unsere Formeln für Streckenlängen, Punktkoordinaten und Flächeninhalte erstellt. Nun sollen die Formeln verwendet werden. Viele verschiedene Fragestellungen können wir damit beantworten:
|
 |
||||||||||||||||||||||||||||||
|
Welchen Flächeninhalt haben die Vierecke bei x = 4? Für welches x ergibt sich eine Streckenlänge von 5 Längeneinheiten? Bei welchem x ergibt sich der maximal mögliche Flächeninhalt? Bei welchem x werden die Vierecke zu Rauten? Bei welchem x werden die Rauten zu Quadraten? Für welche x gibt es überhaupt Vierecke? usw. usw.
|
|||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| y-Werte berechnen | |||||||||||||||||||||||||||||||
|
Eine Formel ist dazu da, etwas zu berechnen, egal ob es eine Formel für Streckenlängen, Punktkoordinaten oder Flächeninhalte ist. Die einfachste Fragestellung ergibt sich, wenn wir mit unseren Formeln einen x-Wert einsetzen und damit einen y-Wert ausrechnen sollen.
|
LE → Längeneinheiten
FE → Flächeneinheiten |
||||||||||||||||||||||||||||||
|
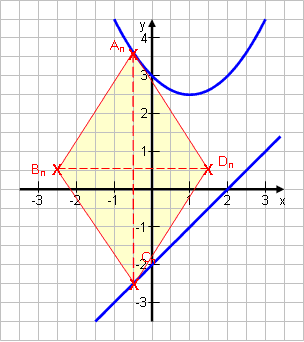
Nehmen wir das zweite Beispiel der vorherigen Lektion:
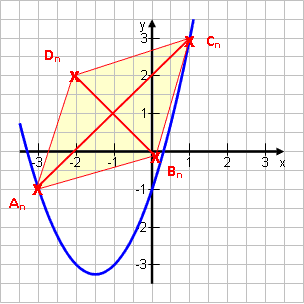
Gegeben ist die Parabel p: y = 0,5x2 – x + 3 und die Gerade g: y = x – 2. An ϵ p ; Cn ϵ g. An und Cn besitzen die gleiche Abszisse x und bilden zusammen mit Punkten Bn und Dn Rauten, deren Diagonale BnDn eine Länge von 4 besitzt Wir hatten eine Formel für die Strecke AnCn und eine Formel für den Flächeninhalt der Rauten erstellt:AnCn (x) = 0,5x2 – 2x + 5A(x) = x2 – 4x + 10 |
|||||||||||||||||||||||||||||||
|
Nun die neuen Fragestellungen:
Welche Streckenlänge AnCn ergibt sich für x = 2? Welcher Flächeninhalt ergibt sich für x = -3? Nichts leichter als das! Einfach x einsetzen und die geforderte Größe ausrechnen:
|
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| x-Werte berechnen (Vorgaben) | |||||||||||||||||||||||||||||||
|
Nun wird es etwas aufwendiger! Wir sollen nicht y- sondern x-Werte berechnen. Die y-Werte gibt man uns vor. Das bedeutet, dass wir nicht einfach nur einsetzen und ausrechnen können, sondern die Formel (sozusagen rückwärts) nach x auflösen müssen.
|


|
||||||||||||||||||||||||||||||
|
Wir bleiben bei unsere Beispiel mit den beiden Formeln für die Streckenlänge und die Fläche:
AnCn (x) = 0,5x2 – 2x + 5A(x) = x2 – 4x + 10 Die neuen Fragestellungen: Für welches x ergibt sich eine Streckenlänge AnCn von 8 LE? Für welches x ergibt sich ein Flächeninhalt von 15 FE? |
|||||||||||||||||||||||||||||||
|
Vom Ansatz her nicht wirklich schwierig, nur etwas aufwendiger! Wir setzen die Vorgaben für y ein:
8 = 0,5x2 – 2x + 5 Es ergibt sich eine Gleichung, die nach x aufgelöst werden muss. Eine Technik, die du inzwischen im Schlaf beherrschst: 8 = 0,5x2 – 2x + 5 | – 8 0 = 0,5x2 – 2x – 3 D = b2 – 4ac = (-2)2 – 4·0,5·(-3) = 10
Eine Streckenlänge AnCn von 8 ergibt sich also für die beiden x-Werte 5,16 und -1,16. Ein Blick auf den Graphen bestätigt zumindest den einen Wert.
|
|||||||||||||||||||||||||||||||
|
Auf die gleiche Weise ermittelt man die x-Werte für die zweite Frage, bei der die Fläche 15 FE werden soll.
15 = x2 – 4x + 10 | – 15 0 = x2 – 4x – 5 D = b2 – 4ac = (-4)2 – 4·1·(-5) = 36
Für die x-Werte 5 und -1 ergibt sich also ein Flächeninhalt von 15. Setzt man die beiden x-Werte zur Probe in die Flächenformel ein, sieht man, dass das auch wirklich stimmt. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Maximale oder minimale Werte | |||||||||||||||||||||||||||||||
|
Eine weitere mögliche Fragestellung: Bei welchem x wird die Streckenlänge oder der Flächeninhalt maximal bzw. minimal?
Für jede Position von An, also für jedes x ergibt sich ja eine andere Streckenlänge und ein anderer Flächeninhalt. In unserem Beispiel sind beide sehr groß für kleine x (links) und für große x (rechts). Irgendwo um x = 1 herum ergibt sich die kürzeste Strecke und damit auch der kleinste Flächeninhalt. |

xS gibt die Stelle an.
yS liefert den Wert der gesuchten Größe an dieser Stelle. 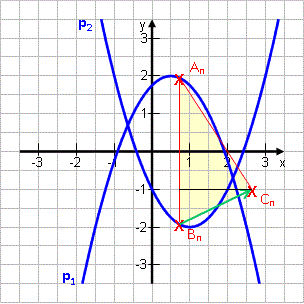
Minimum oder Maximum
bestimmen: Scheitelpunkt S(xS|yS) berechnen. 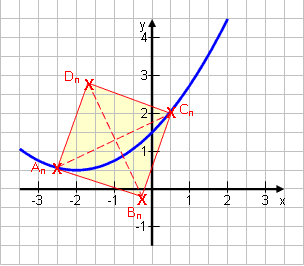
Wurzelfunktion:
xS → ohne Wurzel, yS → mit Wurzel! |
||||||||||||||||||||||||||||||
|
Und wie findet man nun das x, für das sich ein kleinster oder ein größter Wert ergibt? Man bestimmt den Scheitelpunkt S(xS|yS) der entsprechenden Funktion!
Die Frage nach dem Minimum Für welches x ergibt sich die Raute mit dem kleinsten Flächeninhalt? A(x) = x2 – 4x + 10
Antwort: Für x = 2 ergibt sich die Raute mit dem kleinsten Flächeninhalt. Er beträgt dort 6 FE. |
|||||||||||||||||||||||||||||||
|
Ein zweites Beispiel: Maximum
Ebenfalls aus der vorherigen Lektion. Hier ergab sich folgende Formel für die Streckenlänge AnBn :AnBn = -2x2 + 3x + 2,75Wie man am Graphen sieht, gibt es hier für ein bestimmtes x eine größte Streckenlänge, ungefähr bei x = 0,5. Berechnen wir also auch dieses x genau: Die Technik ist wieder die gleiche. Ob größten Wert (Maximum) oder kleinsten (Minimum), immer muss man den Scheitelpunkt der betroffenen Formel berechnen. |
|||||||||||||||||||||||||||||||
|
AnBn = -2x2 + 3x + 2,75
Ergebnis: Für x = 0,75 ist die Streckenlänge maximal. Sie beträgt dort 3,875 LE. |
|||||||||||||||||||||||||||||||
|
Drittes Beispiel: Min/Max bei Wurzelfunktion
|
|||||||||||||||||||||||||||||||
|
Wie geht man eigentlich vor, wenn die Formel eine Wurzelfunktion ist?
In dem Beispiel rechts ergab sich in der vorherigen Lektion eine Rautendiagonale von AnCn = √2,25x² + 15,75x + 36,56Frage: Für welches x wird die Diagonale minimal? |
|||||||||||||||||||||||||||||||
|
Lösung: Die Wurzelfunktion ändert zwar die Werte an sich, aber nicht ihre Größenverhältnisse zueinander. Wenn 9 < 16 ist, dann ist auch √9 < √16 !!!
Deshalb bestimmen wir den kleinsten x-Wert einfach ohne Berücksichtigung der Wurzel!
Auch yS können wir zunächst ohne die Wurzel bestimmen, aber Achtung: Die Formel für die Streckenlänge hat nun mal die Wurzel drüber stehen, also müssen wir sie zum Schluss sehr wohl ziehen:
Minimum: √8,99 = 3 Ergebnis: Es ergibt sich für x = -3,5 die kleinste Diagonale mit einem Wert von 3 LE. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Spezialfälle | |||||||||||||||||||||||||||||||
|
Häufig wird gefragt, wann, also für welches x, ein allgemeiner Fall in einen Spezialfall übergeht.
Für welches x ergibt sich ein gleichschenkliges Dreieck? Wann wird der Drachen zur Raute? Wann die Raute zum Quadrat? Wann das Parallelogramm zum Rechteck? |

Spezialfälle laufen meistens darauf hinaus, einen x-Wert bei vorgegebenem y-Wert zu berechnen. Die Kunst besteht darin, zu erkennen, wie groß der y-Wert sein muss.
|
||||||||||||||||||||||||||||||
|
Erstes Beispiel:
Wieder unser Beispiel von oben. Wir hatten folgende Formel erhalten: AnBn (x) = -2x2 + 3x + 2,75Frage: Für welchen x-Wert x0 ergibt sich ein gleichschenkliges Dreieck A0B0C0 mit der Basis A0C0 ?
|
|||||||||||||||||||||||||||||||
|
Idee: Schau dir den Graphen an. Wenn
AnCn die Basis ist und das Dreieck gleichschenklig, dann müssen die anderen beiden Seiten gleich lang sein:AnBn = BnCn Damit hast du den Ausgangspunkt für deine Rechnung! Da BnCn einfach nur der Vektor
|
|||||||||||||||||||||||||||||||
|
BnCn = √2² + 1² = 2,24Also: 2,24 = AnBn 2,24 = -2x2 + 3x + 2,75 Und schon landen wir wieder an einer Stelle, die wir beherrschen! Gleich Null setzen, Determinante und x1/2 berechnen. 0 = -2x2 + 3x + 0,51 D = 32 – 4·(-2)·0,51 = 13,08
Ergebnis: Für die beiden x-Werte -0,15 und 1,65 ergeben sich gleichschenklige Dreiecke mir der Basis AnCn . |
|||||||||||||||||||||||||||||||
|
Zweites Beispiel:
Unser Beispiel von ganz oben mit AnCn (x) = 0,5x2 – 2x + 5.Frage: Für welches x ergeben sich Quadrate AnBnCnDn? |
|||||||||||||||||||||||||||||||
|
Idee: Bei Quadraten sind beide Diagonalen gleich!
Auch hier ist eine der Diagonalen als Zahl gegeben: BnDn = 4 LE. Ebenso lang muss die andere Diagonale sein: 4 = AnCn (x) 4 = 0,5x2 – 2x + 5 | – 4 0 = 0,5x2 – 2x + 1 D = (-2)2 – 4·0,5·1 = 2 x1 = 3,41 x2 = 0,59 |
|||||||||||||||||||||||||||||||
|
Drittes Beispiel:
Dies ist ein Beispiel aus den Aufgaben der vorherigen Lektion. Frage: Bei welchem x liegt die Strecke AnCn parallel zur x-Achse?Idee: An und Cn liegen waagerecht nebeneinander, wenn sie die gleiche y-Koordinate haben. In der Aufgabe wurden die y-Koordinaten bereits berechnet: yA = x2 + 3x – 2 yC = x2 + 11x + 26 Gleichsetzen: x2 + 3x – 2 = x2 + 11x + 26 | – x2 – 11x + 2 -8x = 28 | : (-8) x = -3,5 |
|||||||||||||||||||||||||||||||