|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Zylinder – das ist Körperberechnung light! Viel gibt es nicht zu berechnen. Volumen und Oberfläche und ab und zu eine Diagonale.
Zylinder spielen allerdings eine wichtige Rolle bei zusammengesetzten Körpern, etwa bei einer Schraube, wo zwei zylindrische Werkstücke mit unterschiedlichem Durchmesser zusammengefügt sind. Dazu mehr in einem späteren Kapitel. Neu in diesem Kapitel ist der Axialschnitt, mit dessen Hilfe man – anstatt des Schrägbildes – alle runden Körper darstellt. |
 |
||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Was ist ein Zylinder? | |||||||||||||||||||||||||||||||
|
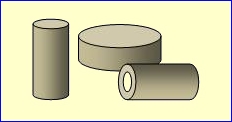
Zylinder sind praktisch runde Prismen. Das heißt, sie besitzen eine runde Grundfläche, die gleichzeitig auch die Deckfläche ist. Die Seitenlinien verlaufen also parallel nach oben, ohne spitzer zu werden. |
|
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Der Zylinder im Axialschnitt | |||||||||||||||||||||||||||||||
|
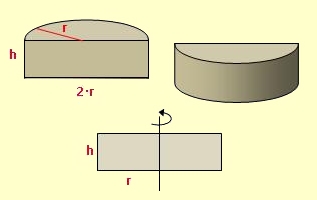
Zylinder wirklich räumlich zu zeichnen, das ist etwas für Künstler! Wir begnügen uns mit einer Hilfskonstruktion, die für Berechnungen viel sinnvoller ist: den Axialschnitt.
Stell dir vor, der Zylinder wird wie ein Kuchen genau in der Hälfte senkrecht durchgeschnitten. Wenn du nun auf die Schnittfläche schaust, hast du einen Axialschnitt vor dir. Und das ist in diesem Fall: ein Rechteck. |
|
||||||||||||||||||||||||||||||
|
Zu einem Axialschnitt gehört außerdem die Rotationsachse mitsamt einem kleinen Drehpfeil, der andeutet, dass es sich um einen 3D-Körper handelt, der um die Achse rotiert.
|
|||||||||||||||||||||||||||||||
|
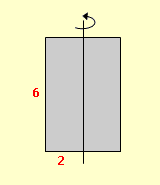
Beispiel :
Zeichne den Axialschnitt eines Zylinders mit r = 2 cm und h = 6 cm. Denke dir den Zylinder aufgeschnitten, so dass du auf ein Rechteck siehst. Alles andere ist ein Kinderspiel. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Volumen und Oberfläche | |||||||||||||||||||||||||||||||
|
Das Volumen berechnet sich wieder wie beim Prisma: Grundfläche mal Höhe. Da die Grundfläche ein Kreis ist, ergibt sich:
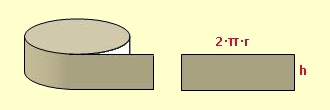
V = G · h = π · r2 · h Die Oberfläche besteht aus zwei Grundflächen und der Mantelfläche. Der Mantel ist – wenn man ihn aufschneidet und ausrollt – ein Rechteck. Dessen Breite ist die Höhe h des Zylinders. Seine Länge ist der Umfang 2·π·r des Zylinders. O = 2·G + M = 2·π·r2 + 2·π·r·h |

|
||||||||||||||||||||||||||||||
|
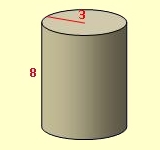
Beispiel:
Berechne Volumen und Oberfläche eines Zylinders mit den Maßen r = 3 cm und h = 8 cm. V = π · 32 · 8 = 226,19 cm3 O = 2·π · 32 + 2·π·3·8 = 207,36 cm2 |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Der Hohl-Zylinder | |||||||||||||||||||||||||||||||
|
Eine Mini-Schwierigkeit kommt hinzu, wenn der Zylinder nicht massiv sondern hohl ist und eine bestimmte Wandstärke besitzt.
In diesem Fall muss man beim Volumen den inneren, hohlen Zylinder vom äußeren Zylinder abziehen. Bei der Oberfläche hat man es mit dem Mantel des äußeren Zylinders zu tun, plus dem Mantel des inneren, plus die beiden Kreisringe, die die Grundfläche bilden. |
Hohl-Zylinder (Rohr)
|
||||||||||||||||||||||||||||||
|
Beispiel:
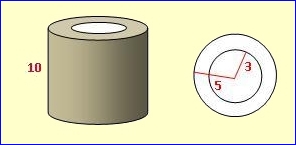
Ein Hohlzylinder der Höhe 10 cm hat einen Außenradius von 5 cm und einen Innenradius von 3 cm. Berechne Volumen und Oberfläche. V1 = π · 52 · 10 = 785,40 cm3 V2 = π · 32 · 10 = 282,74 cm3 V = 785,40 – 282,74 = 502,66 cm3 G = π · (52 – 32) = 50,27 cm2 (Kreisring) M1 = 2·π·5·10 = 314,16 cm2 M2 = 2·π·3·10 = 188,50 cm2 O = 2·50,27 + 314,16 + 188,50 = 603,20 cm2 |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Berechnungen am Zylinder | |||||||||||||||||||||||||||||||
|
Naja, viel gibt es da nicht.
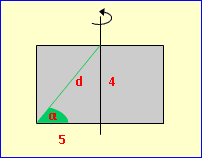
Gegeben sei ein Zylinder mit r = 5 cm und h = 4 cm. Berechne die Länge der Verbindungslinie d von der unteren Kante des Zylinders bis zum Mittelunkt der Deckfläche, sowie den Winkel α, den sie mit der Grundfläche einschließt. d = √5² + 4² = 6,40 cm tan α =
|
|
||||||||||||||||||||||||||||||