|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Pyramiden haben im Gegensatz zu Prismen nur den Boden als Grundfläche. Oben laufen sie stattdessen spitz zu. Alle Seitenkanten treffen sich in der Spitze.
Du solltest dir nicht nur die klassischen ägyptischen Pyramiden als Beispiel vorstellen. Denn die Grundfläche kann nicht nur ein Quadrat sein, sondern auch ein Dreieck, ein Rechteck, ein Drachen, ein Trapez oder jedes andere beliebige n-Eck. |
 |
||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Was macht eine Pyramide aus? | |||||||||||||||||||||||||||||||
|
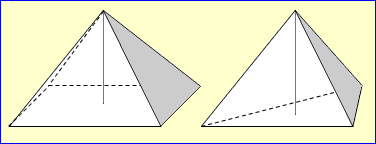
Pyramiden sind Körper, deren Grundfläche ein beliebiges n-Eck ist und dessen Seitenkanten alle in einer Spitze S zusammenlaufen.
Diese Spitze liegt häufig senkrecht über dem Mittelpunkt der Grundfläche. Häufig, aber nicht immer! Bei einigen Pyramiden befindet sich die Spitze senkrecht über einem Eckpunkt, oder irgendwo anders. Die Höhe einer Pyramide ist die Strecke zwischen Spitze und Grundfläche. Sie steht immer senkrecht auf der Grundfläche. |
|
||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Die Pyramide im Schrägbild | |||||||||||||||||||||||||||||||
|
Die Hauptschwierigkeit bei den Schrägbildern besteht im Zeichen der Grundfläche. Man muss aufpassen, dass man die richtige Schrägbildachse nimmt, darf keine Seiten zeichnen, die nicht parallel oder senkrecht zur Zeichenebene liegen und muss an die Verkürzung der nach hinten verlaufenden Linien denken.
Der Rest, das Hochziehen der Kanten und das Verbinden der Punkte, ist einfach. Bei der Pyramide kommen die gleichen Grundflächen vor wie bei den Prismen. Der einzige Unterschied besteht darin, dass sich alle Seitenkanten in der Spitze treffen. Achte im Aufgabentext darauf, wo genau die Spitze liegt! |

|
||||||||||||||||||||||||||||||
|
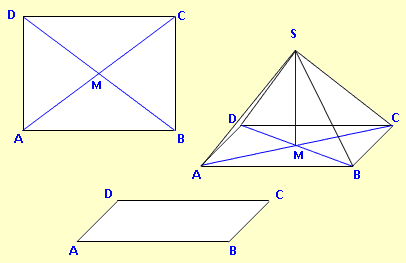
Beispiel 1:
Zeichne das Schrägbild einer Pyramide mit rechteckiger Grundfläche ABCD. AB = 8 cm, BC = 6 cm.Die Spitze S liegt 5 cm über dem Diagonalenschnittpunkt M der Grundfläche. Schrägbildachse ist [BC], ω = 45°, q = 0,5. |
|||||||||||||||||||||||||||||||
|
Nichts Überraschendes in dieser Aufgabe.
Wir zeichnen die Grundfläche wie gewohnt. Dann markieren wir den Schnittpunkt M der beiden Diagonalen und zeichnen die Höhe [MS] ein. Schließlich verbinden wir alle Eckpunkte mit S. |
|||||||||||||||||||||||||||||||
|
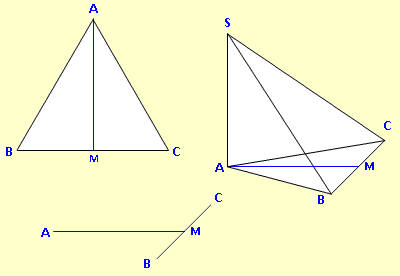
Beispiel 2: Zeichne das Schrägbild der Pyramide ABCS. Die Pyramide besitzt eine Grundfläche ABC in Form eines gleichseitigen Dreiecks. AB = 8 cmDie Spitze S liegt 7 cm über dem Punkt A. Schrägbildachse ist die Dreiecks-Höhe [AM] auf die Seite [AB]. ω = 45°, q = 0,5. |
|||||||||||||||||||||||||||||||
|
Wenn [AM] die Schrägbildachse sein soll, müssen wir zunächst ihre Länge berechnen:
AM = √8² – 4² = 6,93 cmWir beginnen mit dieser Strecke. Am rechten Ende fügen wir [BC] im 45°-Winkel hinzu. Dann die Höhe über A und alles verbinden. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Volumen und Oberfläche | |||||||||||||||||||||||||||||||
|
Das Volumen der Pyramide ist ein Drittel so groß wie das Volumen des entsprechenden Prismas:
V =
Die Oberfläche besteht dieses Mal nur aus einer Grundfläche und der Mantelfläche: O = G + M Dabei besteht die Mantelfläche wegen der Spitze immer aus Dreiecken. Je nach Grundfläche sind es dann drei, vier oder mehr dieser Dreiecke, die außen herum laufen. Eventuell sind sie gleich, oft aber auch verschieden. |

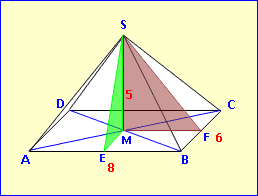
Achte darauf, die verschiedenen Höhen nicht zu verwechseln:
Es gibt die Höhe in der Grundfläche, die Höhen in den Seitendreiecken und die Höhe der Pyramide. 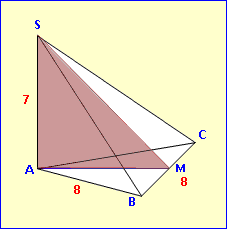
|
||||||||||||||||||||||||||||||
|
Beispiel 1:
Unsere erste Pyramide oben hatte eine rechteckige Grundfläche ABCD mit AB = 8 cm, BC = 6 cm und der Höhe MS = 5 cm.G = 4 · 8 = 32 cm V =
Die Mantelfläche besitzt je zwei gleiche Dreiecke. Um deren Flächeninhalt berechnen zu können, benötigen wir die Höhen der Dreiecksseiten. Die Dreieckshöhe [SF] berechnen wir im Dreieck SFM: SF = √5² + 4² = 6,40 cmAnalog die Dreieckshöhe [SE] im Dreieck SEM: SF = √5² + 3² = 5,83 cmNun die Dreiecksseiten: AABS = 0,5 · 8 · 5,83 = 23,32 cm2 ABCS = 0,5 · 6 · 6,40 = 19,20 cm2 Und schließlich die Oberfläche: O = G + M = 32 + 2·23,32 + 2·19,20 = 117,04 cm2 |
|||||||||||||||||||||||||||||||
|
Beispiel 2:
Unsere zweite Pyramide oben hatte eine gleichseitig-dreieckige Grundfläche ABC mit AB = 8 cm. Die Spitze S lag 7 cm über dem Punkt A.Die Dreieckshöhe der Grundfläche war AM = 6,93 cm.V =
Die Höhe des rechten Dreiecks BCS berechnen wir über das Dreieck AMS: SM = √7² + 6,93² = 9,85 cmDie Höhe der beiden anderen Dreiecke ist in diesem Fall die Pyramidenhöhe [AS]. Also: O = G + M = 0,5·8·6,93 + 0,5·8·9,85 + 2·0,5·8·7 = 123,12 cm2 |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Berechnungen in der Pyramide | |||||||||||||||||||||||||||||||
|
Zusätzlich zu den Höhen der Dreiecksseiten, die wir ja schon berechnet haben, ist man bei der Pyramide oft an den Kantenlängen interessiert. Außerdem an den Winkeln, die die Kanten und die Dreieckshöhen mit der Grundfläche einschließen.
Kanten, Höhen und deren Winkel befinden sich immer in rechtwinkligen Dreiecken, deshalb verwendet man zur Berechnung normalerweise Pythagoras und Tangens. |
Merke:
Kantenlängen: Pythagoras! Bodenwinkel: Tangens! 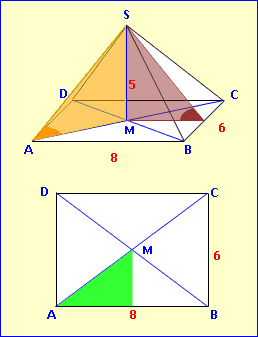 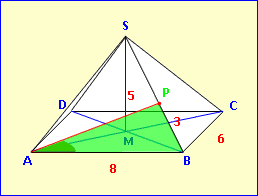 |
||||||||||||||||||||||||||||||
|
Beispiel 1:
Berechne die Länge der Kante [SB] und die Dreieckshöhe [SF], sowie die Winkel, die diese mit der Grundfläche einschließen. Dreieckshöhe: SF = √5² + 3² = 5,83 cmFür die Kantenlänge verwenden wir das Dreieck MAS. Zunächst benötigen wir die halbe Diagonale [AM]. Halbe Diagonale: AM = √4² + 3² = 5 cmKantenlänge: AS = √5² + 5² = 7,07 cmKantenwinkel: tan ∡MAS =
Winkel am Dreieck: tan ∡SFM =
|
|||||||||||||||||||||||||||||||
|
Schwieriger ist es, wenn ein zusätzlicher Punkt an einer festen Stelle auf einer Kante oder Höhe eingeführt wird und man eine Streckenlänge oder einen Winkel zu diesem Punkt berechnen muss.
Da hierbei ganz beliebige Dreiecke entstehen, funktioniert Pythagoras nicht mehr. Stattdessen verwendet man Sinussatz und Kosinussatz. |
|||||||||||||||||||||||||||||||
|
Beispiel 2:
Der Punkt P liege auf der Kante [BS] und ist 3 cm von B entfernt: BP = 3 cm.Berechne die Länge der Strecke [AP] sowie den Winkel ∡BAP. Wir benötigen drei Werte im Dreieck ABP. Zwei haben wir: AB = 8 cm und BP = 3 cm. Als dritte Größe berechnen wir uns den Winkel ∡PBA, der gleichzeitig der Winkel ∡SBA ist. Im vorderen Dreieck ABS gilt mit AS = 7,07 cm:7,072 = 7,072 + 82 – 2·7,07·8·cos ∡SBA ∡SBA = 29,50° Damit können wir AP berechnen:AP 2 = 82 + 32 – 2·8·3·cos 29,50°AP = 5,59 cmUnd den geforderten Winkel: 32 = 82 + 5,592 – 2·8·5,59·cos ∡BAP ∡BAP = 15,35° |
|||||||||||||||||||||||||||||||