| 1.1 |
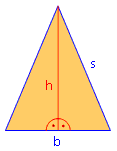
In einem gleichschenkligen Dreieck mit einer Basis von 8 cm sei die Schenkellänge 20 cm. Berechne die Höhe.
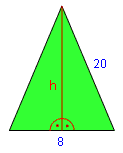 |
|
Lösung
h2 = 202 – 42
h2 = 384 | √
h = 19,60 cm
|
 |
|
| 1.2 |
Berechne die fehlende Seite des abgebildeten Dreiecks.
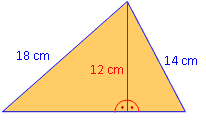 |
|
Lösung
Linkes Teilstück x der Grundseite:
x2 = 182 – 122
x2 = 180 | √
x = 13,42 cm
Rechtes Teilstück y der Grundseite:
y2 = 142 – 122
y2 = 52 | √
y = 7,21 cm
Grundlinie: c = 13,42 + 7,21 = 20,63 cm
|
 |
|
| 1.3 |
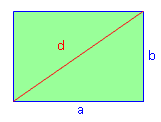
Wie groß ist die Diagonale eines Fensters, das 2,60 m breit und 1,20 m hoch ist? |
|
Lösung
Gefragt ist die Diagonale d eines Rechtecks. 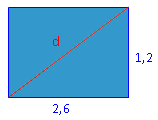 d 2 = 2,6 2 + 1,2 2d 2 = 8,2 | √ d = 2,86 m
|
 |
|
| 1.4 |
Welche Seitenlänge besitzt ein Quadrat, wenn seine Diagonale 1 m beträgt? |
|
Lösung
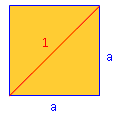 1 2 = a 2 + a 21 2 = 2a 2 | :2 (oder gleich die Formel benutzen) 0,5 = a 2 | √ a = 0,71 m
|
 |
|
| 1.5 |
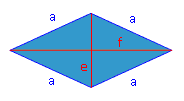
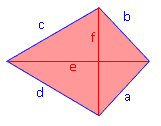
Ein Drachen besitze eine Seitenlänge a = 14 cm und eine Diagonale e = 25 cm, die sich in zwei Teilstücke zu 18 und 7 cm aufteilt. Berechne die Länge der Seite c und der Diagonalen f.
 |
|
Lösung
Teildreieck rechts unten:
| √
| · 2 f = 24,24 cm Teildreieck links oben: c 2 = 12,12 2 + 18 2c 2 = 470,89 | √ c = 21,70 cm
|
 |
|
| 1.6 |
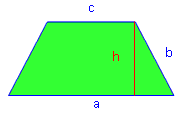
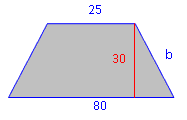
Berechne die Schenkellänge des abgebildeten Trapezes. (Alle Maße in mm.)
 |
|
Lösung
Reststück der Grundlinie unten rechts:
x = 0,5 · (80 – 25) = 0,5·55 = 27,5 mm
b2 = 27,52 + 302
b2 = 1656,25 | √
b = 40,70 mm
|
 |
|
| 1.7 |
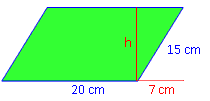
Berechne den Flächeninhalt eines Parallelogramms mit den Seitenlängen 20 und 15 cm, dessen Grundlinien um 7 cm gegeneinander verschoben sind.
 |
|
Lösung
A = g · h
Wir benötigen h!
h2 = 152 – 72
h2 = 176 | √
h = 13,27 cm
A = 20 · 13,27 = 265,40 cm2
|
 |