| 2.1 |
y = 2x – 4
˄ y = -x + 2 |
|
Lösung
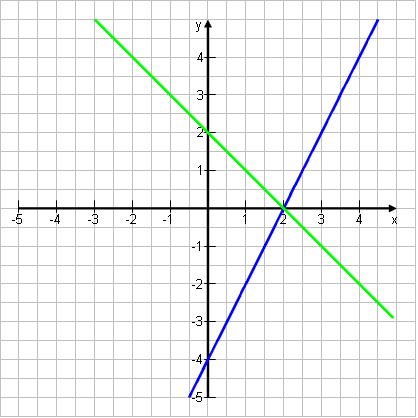 Lösung: S(2|0)
|
 |
|
| 2.2 |
y = -1,5x + 3
˄ y = 0,5x – 3 |
|
Lösung
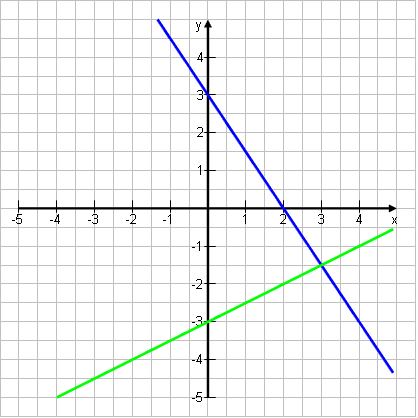 Lösung: S(3|-1,5)
|
 |
|
| 2.3 |
x + y = 5
˄ x – y = 3 |
|
Lösung
x + y = 5 | – x ˄ x – y = 3 | – x y = -x + 5 ˄ -y = -x + 3 | :(-1) y = -x + 5 ˄ y = x – 3 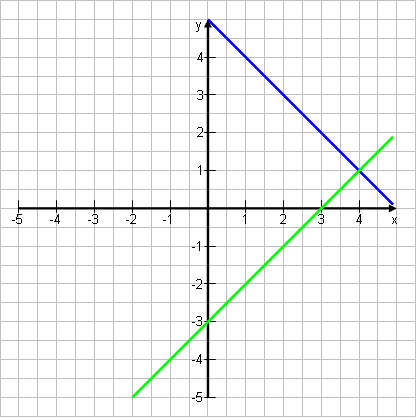 Lösung: S(4|1)
|
 |
|
| 2.4 |
6x = 4 – 2y
˄ x – 0,5y = 1 |
|
Lösung
6x = 4 – 2y | + 2y ˄ x – 0,5y = 1 | – x 6x + 2y = 4 | – 6x ˄ -0,5y = -x + 1 2y = -6x + 4 | : 2 ˄ -0,5y = -x + 1 | :(-0,5) y = -3x + 2 ˄ y = 2x – 2 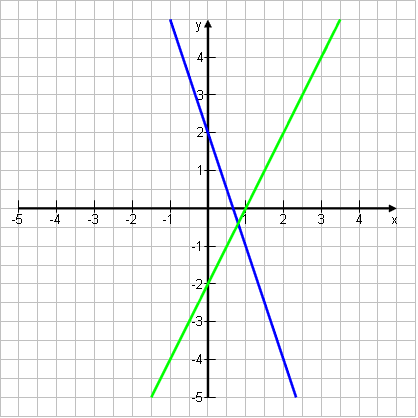 Lösung: S(-0,8|-0,4)
|
 |
|
| 2.5 |
7 = y + 4
˄ x = 0,5y |
|
Lösung
7 = y + 4 | – 4 ˄ x = 0,5y | : 0,5 3 = y ˄ 2x= y 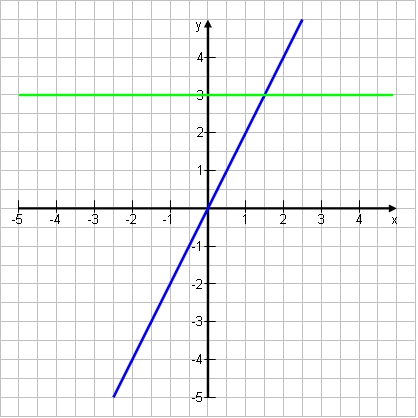 Lösung: S(1,5|3)
|
 |
|
| 2.6 |
Ab wie vielen Minuten wird der Handy-Tarif y = 0,2x + 10 günstiger als der Tarif y = 0,3x + 5? |
|
Lösung
y = 0,2x + 10 ˄ y = 0,3x + 5 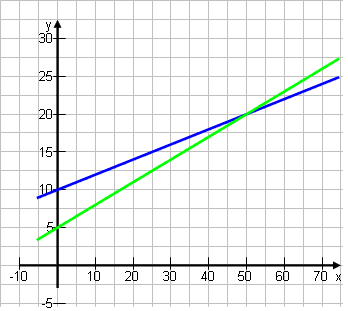 S(50|20) Lösung: Ab 50 Minuten (20 €) wird der erste Tarif günstiger.
|
 |
|
| 2.7 |
Katja und Tim wohnen 50 km voneinander entfernt. Sie wollen sich treffen und fahren gleichzeitig mit dem Fahrrad los. Katja fährt 5 km pro Stunde, Tim 10 km pro Stunde. Wann und wo treffen sich die beiden? |
|
Lösung
y ist die zurückgelegte Strecke, gerechnet ab Katjas Wohnort. x sind die Stunden. Katja: y = 5·x Tim: y = 50 – 10·x 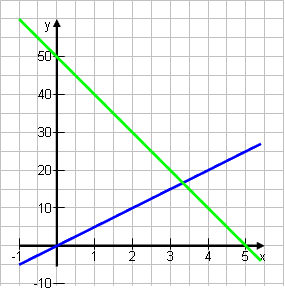 S(3,3|16,7) Lösung: Sie treffen sich nach 3,3 Stunden (3 Std 20 min), 16,7 km von Katja entfernt.
|
 |
|
|




