| 1.1 |
Woran erkennt man lineare Funktionen? |
|
Lösung
Sie enthalten die Variable (x) nur in linearer Form, also als einfaches x, und nicht als x2 oder x3 etc.
|
 |
|
| 1.2 |
Wie sieht die allgemeine Form einer linearen Funktion aus? |
|
Lösung
|
 |
|
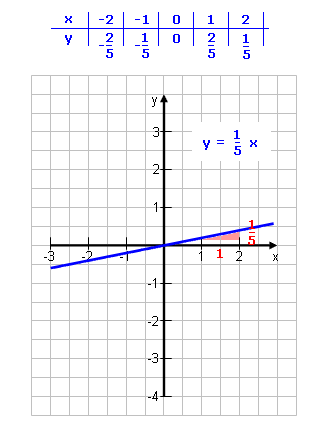
| 1.3 |
Mit welcher Untergruppe befasst sich diese Lektion? |
|
Lösung
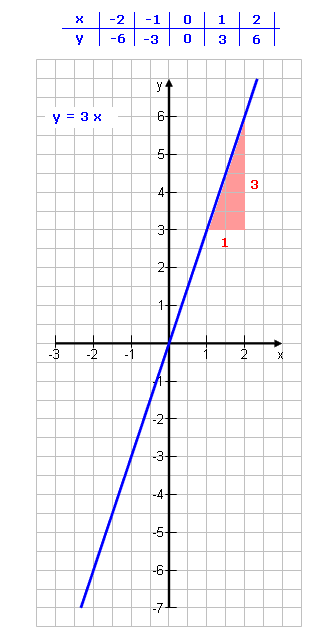
Mit den Funktionen, bei denen t = 0 ist:
y = m·x
|
 |
|
| 1.4 |
Welchen Graphen haben alle lineare Funktionen? |
|
Lösung
|
 |
|
| 1.5 |
Welchen Graphen haben speziell die linearen Funktionen y = m·x? |
|
Lösung
|
 |
|
| 1.6 |
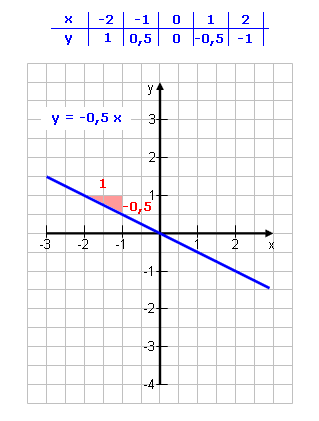
Wie muss die Steigung m aussehen, damit die Gerade fällt? |
|
Lösung
|
 |
|
| 1.7 |
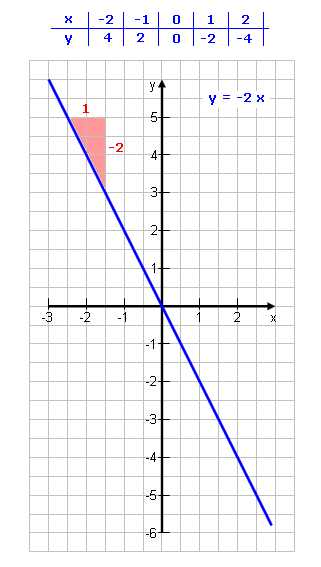
Wie muss die Steigung m aussehen, damit die Gerade steigt? |
|
Lösung
|
 |
|
| 1.8 |
Wann ergibt sich eine flache Gerade? |
|
Lösung
|
 |
|
| 1.9 |
Wann ergibt sich eine steile Gerade? |
|
Lösung
|
 |
|
| 1.10 |
Was ist ein Steigungsdreieck? |
|
Lösung
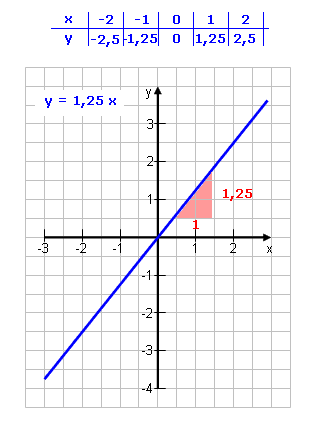
Das Dreieck, das sich ergibt, wenn man von einem beliebigen Punkt aus 1 nach rechts geht und die Steigung m nach oben.
|
 |
|
| 1.11 |
Wie zeichnet man die Steigung ein, wenn m ein Bruch ist? |
|
Lösung
Nenner nach rechts, Zähler nach oben/unten.
|
 |
|
| 1.12 |
Wie geht man vor, wenn m eine Dezimalzahl ist? |
|
Lösung
10 nach rechts, Anzahl Zehntel nach oben/unten.
|
 |
|
| 1.13 |
Muss man Kästchen zählen oder Einheiten (cm)? |
|
Lösung
Egal. Wichtig ist nur, dass man sowohl nach rechts als auch nach oben/unten die gleiche Variante wählt.
|
 |
|
| 1.14 |
Wie viele Punkte muss man eigentlich nur berechnen, um eine Gerade eindeutig zeichnen zu können? |
|
Lösung
|
 |