mathepanik.de

Lektion
Verknüpfungen

Themenübersicht

zurück zur Lektion

Die Bedeutung der einzelnen Begriffe

1.1	Welche der beiden Bedingungen müssen erfüllt sein, wenn sie mit einem ODER verknüpft sind?		Lösung Wenigstens eine der Bedingungen.

1.2	Welche der beiden Bedingungen müssen erfüllt sein, wenn sie mit einem UND verknüpft sind?		Lösung Beide Bedingungen müssen erfüllt sein.

1.3	Welches Symbol steht für UND?		Lösung ˄

1.4	Welches Symbol steht für ODER?		Lösung ˅

1.5	Ist die Schnittmenge oder die Vereinigungsmenge die Lösung bei einer UND-Verknüpfung?		Lösung Die Schnittmenge.

1.6	Ist die Schnittmenge oder die Vereinigungsmenge die Lösung bei einer ODER-Verknüpfung?		Lösung Die Vereinigungsmenge.

Zeichne zunächst beide Teilmengen und lege zuletzt fest, welche Punkte zur Lösungsmenge gehören.

2.1	Alle Punkte, die mehr als 3 cm Abstand und weniger als 5 cm Abstand von A haben.		Lösung 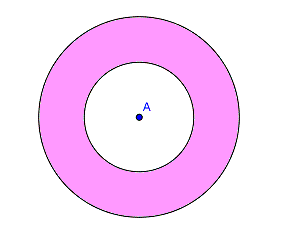Die Lösung ist der Ring zwischen den beiden Kreisen.

2.2	Alle Punkte, die mehr als 3 cm Abstand ODER weniger als 5 cm Abstand von A haben.		Lösung 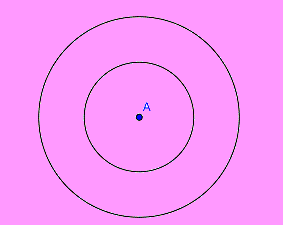Die Lösung ist die gesamte Ebene. Denn JEDER Punkt erfüllt eine der beiden Aussagen. Die Kreislinien selbst gehören ebenfalls dazu.

2.3	Alle Punkte, die weniger als 3 cm Abstand ODER mehr als 5 cm Abstand von A haben.		Lösung 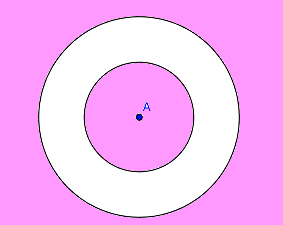Die Lösung ist die komplette Ebene mit Ausnahme des Kreisrings.

2.4	Alle Punkte, die weniger als 3 cm Abstand von B haben und gleich weit entfernt von A und B sind. (A ist 4 cm von B entfernt.)		Lösung 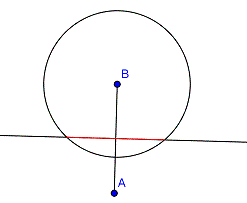Die Lösung ist der Teil der Mittelsenkrechten, der innerhalb des Kreises liegt.

2.5	Alle Punkte, die gleich weit von den Geraden g und h entfernt sind und weniger als 2 cm vom Punkt A. (g und h haben einen Abstand von 3 cm.)		Lösung 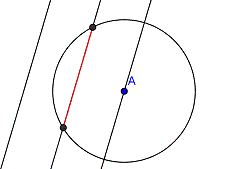Die Lösung ist der Teil der Mittelparallelen, der innerhalb des Kreises liegt.

2.6	Alle Punkte, die näher an h als an g liegen und gleich weit von k wie von h entfernt sind.	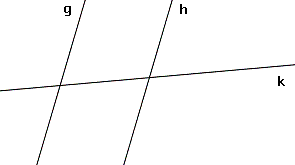	Lösung 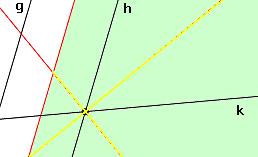Die Lösung (gelb) ist der Teil der Winkelhalbierenden von h und k, der innerhalb der rechten Halbebene liegt, die durch die Mittelparallele von g und h gebildet wird.

2.7	Alle Punkte, die 3 cm von P und 4,5 cm von Q entfernt sind. (Abstand PQ = 2 cm)	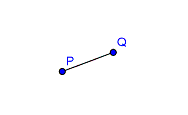	Lösung 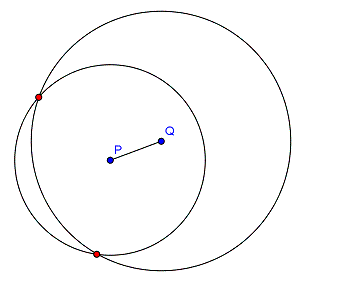Die Lösung sind die beiden Schnittpunkte der Kreise um P und Q.

2.8	Alle Punkte, die näher an h als an g liegen und weniger als 5 cm von P entfernt sind. (Abstand von P zu g: d(P; g) = 2,5 cm.)	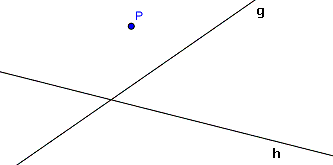	Lösung 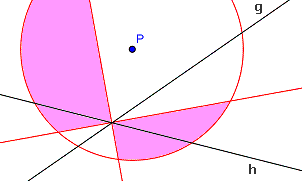Die Lösung ist der Teil innerhalb des Kreises, der auf der richtigen Seite der Winkelhalbierenden liegt.

2.9	Alle Punkte, die näher an g als an h liegen ODER weniger als 5 cm von P entfernt sind.		Lösung 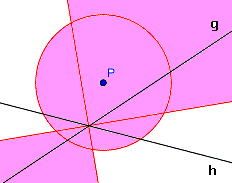Die Lösung ist das Innere des Kreises und zusätzlich die richtige Seite der Winkelhalbierenden.

Die mathematische Schreibweise.

Welche Bedeutung haben die folgenden Beschreibungen?

3.1	{P \| PC > 5 cm ˄ PC < 7 cm}		Lösung Die Menge aller Punkte P, deren Abstand von C größer als 5 cm und kleiner als 7 cm ist. Das ist ein Kreisring.

3.2	{P \| PC = PD ˄ PC < 5 cm}		Lösung Die Menge aller Punkte P, die gleich weit von C wie von D entfernt sind\ (Mittelsenkrechte)\ und weniger als 5 cm Abstand von C haben (Kreisinneres). Das ist der Teil der Mittelsenkrechten, der innerhalb des Kreises liegt.

3.3	{P \| d(P; g) = d(P; h) ˄ PA > 3 cm}		Lösung Die Menge aller Punkte P, die den gleichen Abstand zu g und zu h haben (Mittelparallele oder Winkelhalbierende) und mehr als 3 cm von A entfernt sind (Kreisäußeres). Das ist der Teil der Mittelparallelen oder Winkelhalbierenden, der außerhalb des Kreises liegt.

3.4	{P \| d(P; g) < 3 cm ˅ d(P; g) > 6 cm}		Lösung Die Menge aller Punkte, deren Abstand zu g weniger als 3 cm oder mehr als 6 cm beträgt. Dies ist der Streifen innerhalb des Parallelenpaares von 3 cm und zusätzlich das Äußere des Parallelenpaares von 6 cm.

Fehler gefunden oder Anregungen?

zurück zur Lektion