Lektion
   Trapeze   
Hilfe
Panik-Test
Themenübersicht
zurück zur Lektion
Alles verstanden?
1.1 Wodurch zeichnet sich ein Trapez aus?   Lösung
1.2 Was ist das besondere an einem gleichschenkligen Trapez?   Lösung
1.3 Wie lautet die Formel zur Berechnung des Flächeninhalts eines Trapezes?   Lösung
1.4 Wie lautet die Formel zur Berechnung des Flächeninhalts eines Drachen oder einer Raute?   Lösung
1.5 Wie lautet die Formel für die Fläche eines Parallelogramms?   Lösung
1.6 Wie lautet die Formel für die Fläche eines Dreiecks?   Lösung
Berechne die gesuchte Größe
2.1 Ein Trapez besitze die Maße a = 7 cm, b = 5 cm, c = 9 cm, d = 5 cm und h = 4 cm. Berechne seinen Flächeninhalt.   Lösung
2.2 Ein Trapez mit 44 cm2 Flächeninhalt besitze Grundlinien von 5,2 und 7,3 cm. Wie groß ist seine Höhe?   Lösung
2.3 Ein Trapez mit a = 23 cm und h = 12 cm habe einen Flächeninhalt von 180 cm2. Berechne die zweite Grundlinie c.   Lösung
2.4 A = 200 cm2; b = 6 cm; d = 14 cm ; b | | d. Berechne h.   Lösung
2.5 A = 130 cm2; d = 5,5 cm; h = 8,2 cm ; b | |d. Berechne b.   Lösung
Nun wird es etwas komplizierter:
3.1 Ein Trapez besitzt einen vier Mal so großen Flächeninhalt wie ein Parallelogramm mit Grundseite 7 cm und Höhe 3,4 cm. Wie hoch ist das Trapez, wenn es die Grundlinien 2,1 cm und 4,5 cm besitzt?   Lösung
3.2 Ein Drachen mit den Diagonalen e = 6,1 cm und f = 14,7 cm besitzt einen doppelt so großen Flächeninhalt wie ein Trapez, dessen eine Grundlinie 7,2 cm und dessen Höhe 2,3 cm lang ist. Wie lang ist die zweite Grundlinie des Trapezes?   Lösung
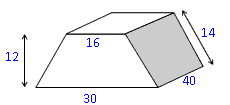
3.3 Berechne die Oberfläche des Holzklotzes. Alle Maße in cm.

   Lösung
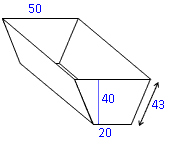
3.4 Der 1,20 m lange Wassertrog soll innen gestrichen werden. Für wie viel m2 muss Farbe besorgt werden? (Alle Maße in cm)

   Lösung
Fehler gefunden oder Anregungen?
zurück zur Lektion