mathepanik.de

Lektion
Formeln für senkrechte Strecken

1.1	Gegeben seien die Parabel p: y = -x² + 4x – 5 und die Gerade g: y = x – 1 . A_n ϵ p ; B_n ϵ g ; A_n und B_n haben die gleiche Abszisse x. Berechne den Abstand A_nB_n in Abhängigkeit von x.	Lösung Oben minus Unten: Gerade minus Parabel A_nB_n (x) = x – 1 – (-x² + 4x – 5) = x – 1 + x² – 4x + 5 = x² – 3x + 4

1.2	Gegeben seien die Parabel p: y = x² + 2x – 1 und die Gerade g: y = -0,5x + 1 . A_n ϵ p ; B_n ϵ p ; A_n und B_n haben die gleiche Abszisse x. Berechne den Abstand A_nB_n in Abhängigkeit von x im Bereich [-3,13 ; 0,64].	Lösung Oben minus Unten: Gerade minus Parabel A_nB_n (x) = -0,5x + 1 – (x² + 2x – 1) = -0,5x + 1 - x² – 2x + 1 = -x² – 2,5x + 2

1.3	Gegeben seien die Parabel p₁: y = 0,5x² – 2x + 1 und die Parabel p₂: y = -x² + 2x + 1 A_n ϵ p₁ ; B_n ϵ p₂ ; A_n und B_n haben die gleiche Abszisse x. Berechne den Abstand A_nB_n in Abhängigkeit von x im Bereich [0 ; 2,67].	Lösung Oben minus Unten: p₂ minus p₁ A_nB_n (x) = -x² + 2x + 1 – (0,5x² – 2x + 1) = -x² + 2x + 1 – 0,5x² + 2x – 1 = -1,5x² + 4x

1.4	Gegeben seien die Parabel p₁: y = 0,5x² – 2x + 4 und die Parabel p₂: y = x² – 4x + 2 A_n ϵ p₁ ; B_n ϵ p₂ ; A_n und B_n haben die gleiche Abszisse x. Berechne den Abstand A_nB_n in Abhängigkeit von x im Bereich [-0,83 ; 4,83].	Lösung Oben minus Unten: p₂ minus p₁ A_nB_n (x) = 0,5x² – 2x + 4 – (x² – 4x + 2) = 0,5x² – 2x + 4 – x² + 4x – 2 = -0,5x² + 2x + 2

2.1	Gegeben seien die Parabel p: y = -x² + 2x + 2 und die Gerade g: y = -2x + 3 . A_n ϵ p ; B_n ϵ g ; A_n und B_n haben die gleiche Abszisse x. Skizziere die Graphen und berechne den Abstand A_nB_n in Abhängigkeit von x im Bereich [0,37 ; 3,73].	Lösung Oben minus Unten: Parabel minus Gerade A_nB_n (x) = -x² + 2x + 2 – (-2x + 3) = -x² + 2x + 2 + 2x – 3 = -x² + 4x – 1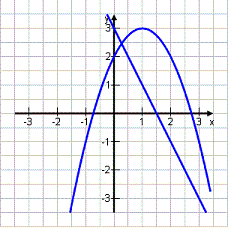

2.2	Gegeben seien die Parabel p: y = 2x² – 8x + 7 und die Gerade g: y = -1,5 . A_n ϵ p ; B_n ϵ g ; A_n und B_n haben die gleiche Abszisse x. Skizziere die Graphen und berechne den Abstand A_nB_n in Abhängigkeit von x.	Lösung Oben minus Unten: Parabel minus Gerade A_nB_n (x) = 2x² – 8x + 7 – (-1,5) = 2x² – 8x + 7 + 1,5 = 2x² – 8x + 8,5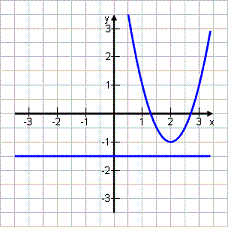

2.3	Gegeben seien die Parabel p₁: y = -0,5x² + x + 0,5 und die Parabel p₂: y = 1,5x² – 3x + 2,5 A_n ϵ p₁ ; B_n ϵ p₂ ; A_n und B_n haben die gleiche Abszisse x. Skizziere die Graphen und berechne den Abstand A_nB_n in Abhängigkeit von x.	Lösung Oben minus Unten: p₂ minus p₁ A_nB_n (x) = 1,5x² – 3x + 2,5 – (-0,5x² + x + 0,5) = 1,5x² – 3x + 2,5 + 0,5x² – x – 0,5 = 2x² – 4x + 2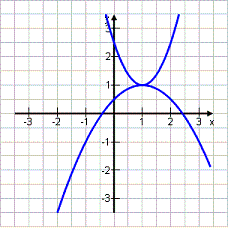

2.4	Gegeben seien die Parabel p₁: y = x² + 2x – 1 und die Parabel p₂: y = 0,5x² + x –1,5 A_n ϵ p₁ ; B_n ϵ p₂ ; A_n und B_n haben die gleiche Abszisse x. Skizziere die Graphen und berechne den Abstand A_nB_n in Abhängigkeit von x.	Lösung Oben minus Unten: p₁ minus p₂ A_nB_n (x) = x² + 2x – 1 – (0,5x² + x – 1,5) = x² + 2x – 1 – 0,5x² – x + 1,5 = 0,5x² + x + 0,5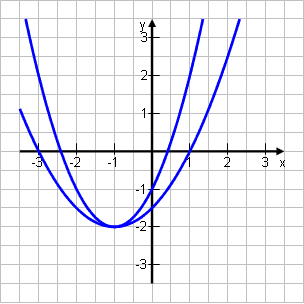

Fehler gefunden oder Anregungen?