| 3.1 |
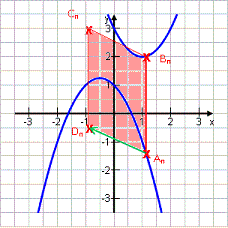
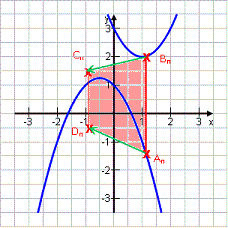
Gegeben seien die Parabel p1: y = -x2 – x + 1 und die Parabel p2: y = x2 – 2x + 3
An ϵ p1 ; Bn ϵ p2 ; An und Bn haben die gleiche Abszisse x und bilden dieses Mal mit den Punkten Cn und Dn Trapeze, wobei gilt:
und
.
Es ergeben sich folgende Formeln:
CnDn (x) = 2x2 – x + 0,5
A(x) = 4x2 – 2x + 2,5
 |
|
|
| 3.2 |
Für welches x besitzen die Trapeze die kürzeste Strecke CnDn und wie groß ist diese dann? |
|
Lösung
CnDn (x) = 2x 2 – x + 0,5
Mit x = 0,25 ist die Strecke CnDn minimal. Sie beträgt dort 0,375 LE.
|
 |
|
| 3.3 |
Für welches x besitzen die Trapeze den kleinsten Flächeninhalt und wie groß ist dieser dann? |
|
Lösung
A(x) = 4x 2 – 2x + 2,5
Für x = 0,25 ist der Flächeninhalt minimal. Er beträgt dort 2,25 FE.
|
 |
|
| 3.4 |
Noch einmal die Aufgabe von ganz oben:
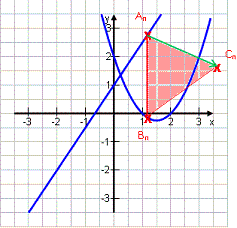
Gegeben seien die Gerade g: y = 1,5x + 1 und die Parabel p: y = x2 – 3x + 2.
An ϵ g ; Bn ϵ p ; An und Bn haben die gleiche Abszisse x. Die Punkte Cn ergeben sich durch den Vektor
.
Es ergeben sich folgende Formeln:
AnBn (x) = -x2 + 4,5x – 1
A(x) = -1,25x2 + 5,63x – 1,25
 |
|
|
| 3.5 |
Für welches x besitzen die Dreiecke die längste Strecke AnBn und wie groß ist diese dann? |
|
Lösung
AnBn (x) = -x 2 + 4,5x – 1
Mit x = 2,25 ist die Strecke AnBn maximal. Sie beträgt dort 4,06 LE.
|
 |
|
| 3.6 |
Für welches x besitzen die Dreiecke den größten Flächeninhalt und wie groß ist dieser dann? |
|
Lösung
A(x) = -1,25x 2 + 5,63x – 1,25
| yS = c – | | = -1,25 – | | = 5,09 |
Für x = 2,25 ist der Flächeninhalt maximal. Er beträgt dort 5,09 FE.
|
 |
|
| 3.7 |
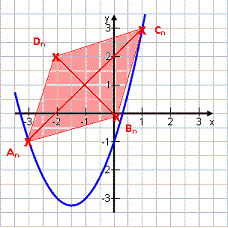
Gegeben sei die Parabel p mit p: y = x2 + 3x – 2
An und Cn liegen auf p, wobei Cn gegenüber An um 4 nach rechts verschoben ist. Die Abszisse der Punkte An ist x. An und Cn bilden mit den Punkten Bn und Dn Rauten, deren Diagonale BnDn 3 Längeneinheiten lang ist.
Für die Fläche der Rauten ergibt sich folgende Formel:
A(x) = 1,5·√64x² + 448x + 800
 |
|
|
| 3.8 |
Für welches x besitzen die Rauten den kleinsten Flächeninhalt und wie groß ist dieser dann? |
|
Lösung
A(x) = 1,5· √64x² + 448x + 800A(x) ist minimal, wenn der Term unter der Wurzel minimal ist:
Der Wert der Fläche an dieser Stelle ergibt sich aus A(x S) = 1,5· √yS.
Fläche: A(x S) = 1,5· √yS = 1,5· √16 = 6 Für x = -3,5 ist der Flächeninhalt minimal. Er beträgt dort 6 FE.
|
 |
|
|