mathepanik.de

Lektion
Prismen

1.1

Zeichne ein Schrägbild des Quaders ABCDEFGH mit der Grundfläche ABCD.

= 10 cm,

= 5 cm und

= 6 cm.

[AB] liegt auf der Schrägbildachse.
ω = 45° ; q = 0,5

Lösung

1.2

Berechne Volumen und Oberfläche des Quaders.

Lösung

1.3

Berechne die Flächendiagonalen [AC] und [AF].

Lösung

1.4

Berechne die Raumdiagonalen [AG] und [BH].

Lösung

1.5

Berechne die Winkel ∠BAC und ∠CAG

Lösung

1.6

Berechne den Winkel ∠FAG zwischen der Raum- und der Flächendiagonalen.

Lösung

2.1

Zeichne ein Schrägbild des Prismas ABCDEF. Die Grundfläche ABC des Prismas ist ein rechtwinkliges Dreieck mit dem rechten Winkel bei B.

Es gilt:

= 8 cm,

= 6 cm und Prismenhöhe

= 4 cm.

[AB] liegt auf der Schrägbildachse.
ω = 60° ; q = 0,5

Lösung

2.2

Berechne Volumen und Oberfläche des Prismas.

Lösung

2.3

Berechne die Flächendiagonalen [AE] und [CE].

Lösung

2.4

Berechne die Höhe [HB] im Bodendreieck ABC, die auf AB senkrecht steht.

Lösung

2.5

Berechne die Länge der Strecke [EH].

Lösung

2.6

Berechne den Flächeninhalt des Dreiecks AEC.

Lösung

3.1	Zeichne ein Schrägbild des Prismas ABCDEF. Die Grundfläche ABC des Prismas ist ein gleichschenkliges Dreieck mit der Basis AB. Es gilt: AB = 8 cm, BC = AC = 6 cm. Das Prisma ist 5 cm hoch. Achtung: Schrägbildachse ist nicht die Seite des Dreiecks sondern die Höhe [CM] auf die Basis. (M ist der Mittelpunkt der Basis AB) (C links zeichnen, M rechts.) ω = 45° ; q = 0,5	Lösung Grundfläche: 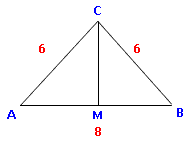Zum zeichnen der Grundfläche im Schrägbild brauchen wir die Höhe [CM]: CM ^² = 6² – 4² \| √ EH = 4,47 cm Zuerst wird [CM] gezeichnet. An den Punkt M kommt nun die Basis [AB], wegen der Schräge nur mit 4 cm gezeichnet und davon die Hälfte nach oben, die Hälfte nach unten.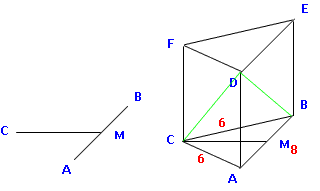

3.2	Berechne Volumen und Oberfläche des Prismas.	Lösung G = 0,5 · 8 · 4,47 = 17,88 cm² V = 17,88 · 5 = 89,4 cm³ O = 2·17,88 + 2·6·5 + 8·5 = 135,76 cm²

3.3	Berechne die Flächendiagonalen [CD] und [BD].	Lösung CD ^² = 6² + 5² \| √ CD = 7,81 cm BD ^² = 8² + 5² \| √ BD = 9,43 cm

3.4	Berechne alle Winkel im Dreieck CBD.	Lösung Achtung, dieses Dreieck hat keinen rechten Winkel. Dafür haben wir aber alle Seitenlängen. Deshalb bietet sich der Kosinussatz an. γ bei C, β bei B und δ bei D: BD ^² = BC ^² + CD ^² – 2· BC · CD ·cos γ 9,43² = 6² + 7,81² – 2·6·7,81·cos γ γ = 85,06° 7,81² = 6² + 9,43² – 2·6·9,43·cos β β = 55,60° α = 180° – 85,06° – 55,60° = 39,34°