|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||
|
Die Gesetzmäßigkeiten, die bei der zentrischen Streckung herrschen, lassen sich hervorragend für Berechnungen in geometrischen Figuren verwenden.
Es geht dabei um solche Situationen, bei denen zwei Figuren "ähnlich" sind, also die gleiche Form besitzen, aber unterschiedlich groß sind. Man stellt sich dann vor, dass die eine Figur durch eine zentrische Streckung aus der anderen Figur hervorgegangen ist. |
 |
|||||||||||||||||||||||||||
|
Die Lehrsätze, die bei der Berechnung helfen, hat man ein wenig umformuliert, damit sie leichter anzuwenden sind. In einigen Bundesländern heißen sie Vierstreckensätze, in anderen Strahlensätze.
|
||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
| Die Vierstreckensätze/Strahlensätze | ||||||||||||||||||||||||||||
|
Voraussetzung:
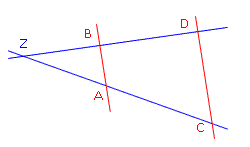
Zwei sich schneidende Geraden ("Strahlen") werden durch zwei parallele Geraden geschnitten. Diese Formulierung ist wirklich grausam! Man kann sich zunächst nicht viel darunter vorstellen. Deshalb hier ein paar Beispiele. 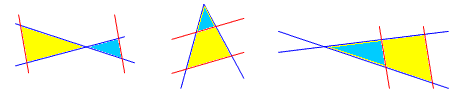 Wie du siehst, entstehen dabei immer zwei Dreiecke, die die gleiche Form haben, aber unterschiedlich groß sind (zwei "ähnliche" Dreiecke). Das kleinere Dreieck (blau) liegt oft in oder auf dem großen Dreieck (gelb), verdeckt es dadurch teilweise. Das große entsteht sozusagen durch Vergrößerung aus dem kleineren. |
|
|||||||||||||||||||||||||||
|
Die Sätze:
Unter diesen Bedingungen gilt: Das Verhältnis zweier Seiten in der einen Figur ist genauso groß, wie das Verhältnis der entsprechenden Seiten in der anderen Figur. Am Besten, wir sehen uns ein Beispiel an: Für die beiden Dreiecke rechts gelten folgende Beziehungen:
|
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
| Noch einmal ganz langsam | ||||||||||||||||||||||||||||
|
Du hast keine Chance, dir diese Gleichungen auswendig zu merken, zumal du niemals die Punkte A, B, C und D in diesen Positionen finden wirst. Nein, du musst dir definitiv die Bedeutung der Sätze merken!
|
|
|||||||||||||||||||||||||||
|
Erster Satz:
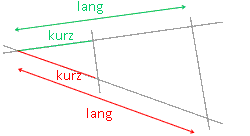
Kurzes Stück zu langem Stück auf dem ersten Strahl wie kurzes Stück zu langem Stück auf dem zweiten Strahl. Gar nicht schwer! Zweiter Satz:
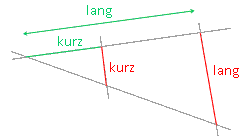
Kurzes Stück zu langem Stück auf dem ersten Strahl (oder dem zweiten!) wie kurze Parallele zu langer Parallele. Auch nicht schwer. Dritter Satz:
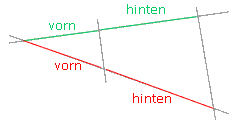
Vorderes Stück zu hinterem Stück auf dem ersten Strahl wie vorderes Stück zu hinterem Stück auf dem zweiten Strahl. Erst recht nicht schwer! |
||||||||||||||||||||||||||||
|
Hier ein letztes Mal in aller Kürze:

|
||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||
| Beispiele | ||||||||||||||||||||||||||||
|
Der Vierstreckensatz/Strahlensatz dient dazu, unbekannte Strecken auszurechnen. Mal sehen, wie man das anstellt:
|
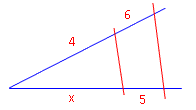
(Alle Angaben in cm.)
    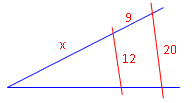
|
|||||||||||||||||||||||||||
|
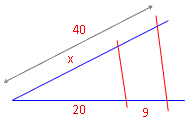
Beispiel 1:
Wir suchen das linke, untere Teilstück x. Spruch: Vorn zu hinten wie vorn zu hinten.
|
||||||||||||||||||||||||||||
|
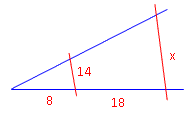
Beispiel 2:
Wir suchen wieder x. Spruch: Kurz zu lang wie kurz zu lang.
Vorsicht! Mit "lang" ist die lange Strecke ab der Spitze gemeint, nicht nur das vordere oder hintere Stück.!!! |
||||||||||||||||||||||||||||
|
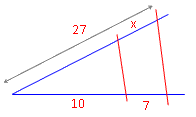
Beispiel 3:
Spruch: Lang zu kurz wie lang zu kurz (mit den Parallelen).
Ja, da staunst du! Die Sprüche sind Klasse. Vor allem, weil man sie auch umdrehen darf. Formuliere die Sache immer so, dass du mit x beginnst. Das spart eine Menge Umformungen und Fehler. Aber auch hier: Vorsicht! Mit "lang" ist immer die lange Strecke ab der Spitze gemeint!!! Das hintere Stück heißt "hinten"! :O) |
||||||||||||||||||||||||||||
|
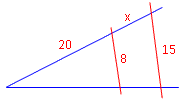
Beispiel 4:
Spruch: Hinten zu lang wie hinten zu lang. Ach, diesen Spruch kennst du nicht? ;O) Egal, es klappt immer, solange man rechts und links vom Gleichheitszeichen die gleichen Teilstücke miteinander ins Verhältnis setzt.
|
||||||||||||||||||||||||||||
|
Beispiel 5:
Schwierig. Da die beiden Parallelen gegeben sind, müssen wir sie zu kurz und lang ins Verhälnis setzen (nicht zu vorn und hinten)! Spruch: Lang zu kurz wie lang zu kurz.
x = 17,5 cm |
||||||||||||||||||||||||||||
|
Beispiel 6:
Widerlich! Einfach widerlich! Spruch: Kurz zu lang wie kurz zu lang.
x = 0,6 · (x + 9) x = 0,6x + 5,4 | – 0,6x 0,4x = 5,4 | : 0,4 x = 13,5 cm widerlich! |
||||||||||||||||||||||||||||