|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||
|
Immer noch um rechtwinklige Dreiecke. Zeichnet man die Höhe auf die Hypotenuse ein, ergeben sich zwei neue rechtwinklige Teildreiecke, in denen ganz besondere Beziehungen herrschen.
|
 |
|||||||||||||||||||||||||

|
||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||
| Der Höhensatz und die Kathetensätze | ||||||||||||||||||||||||||
|
Es geht nach wie vor um rechtwinklige Dreiecke. Aber jetzt wird die Höhe eine entscheidende Rolle spielen.
Da unser Dreieck rechtwinklig ist, ist jede Kathete ja bereits die Höhe der anderen Kathete. Nur die Hypotenuse hat eine eigene Höhe. Diese Höhe teilt den rechten Winkel und unterteilt die Hypotenuse in zwei Stücke p und q. |
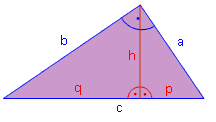


Beachte, dass p typischerweise rechts liegt und q links. Dies wurde so vereinbart, damit p bei seiner Kathete a liegt und q bei seiner Kathete b.
|
|||||||||||||||||||||||||
|
Für genau diese Situation – die Höhe teilt die Hypotenuse im rechtwinkligen Dreieck – gelten folgende Sätze:
Höhensatz: h2 = p · q
Dabei gilt natürlich: p + q = c |
||||||||||||||||||||||||||
|
Erläuterung:
h2 = p · q Multipliziert man die beiden Teilstücke der Hypotenuse miteinander, erhält man h2. a2 = c · p Die ganze Hypotenuse c mal das Teilstück p, das bei a liegt, ergibt a2. b2 = c · p Die ganze Hypotenuse c mal das Teilstück q, das bei b liegt, ergibt b2. |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Beispiele | ||||||||||||||||||||||||||
|
Beispiel 1:
Ein rechtwinkliges Dreieck besitze die Hypotenuse c = 10 cm sowie die Hypotenusen-Teilstücke p = 4 cm und q = 6 cm. Berechne die Katheten a und b und die Höhe h. a2 = c · p a2 = 10 · 4 = 40 | √ a = 6,32 cm b2 = c · q b2 = 10 · 6 = 60 | √ b = 7,75 cm h2 = p · q h2 = 4 · 6 = 24 | √ h = 4,90 cm |
Eigentlich eine nette mathematische Spielerei: Du erhältst zwei Größen und einen Haufen Formeln und sollst nun versuchen, die restlichen Werte zu berechnen.
a2 = c · p b2 = c · q
Die Hypotenuse c mal das Stück, das bei der Kathete liegt! |
|||||||||||||||||||||||||
|
Beispiel 2:
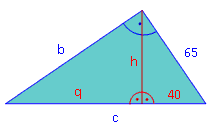
Berechne alle fehlenden Größen im abgebildeten Dreieck (alle Maße in cm). c berechnen über den Kathetensatz von a: a2 = c · p 652 = c · 40 | : 40 c = 105,63 cm q = c – p = 105,63 – 40 = 65,63 cm b über den Kathetensatz: b2 = c · q b2 = 105,63 · 65,63 | √ b = 83,26 cm h über den Höhensatz (oder über Pythagoras im rechten Teildreieck): h2 = p · q h2 = 40 · 65,63 | √ h = 51,24 cm |
||||||||||||||||||||||||||
|
Beispiel 3:
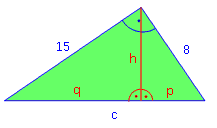
Das gleiche Spiel noch einmal: Berechne alle fehlenden Größen. (Angaben in cm) c über Pythagoras: c2 = a2 + b2 c2 = 152 + 82 | √ c = 17 cm p über den Kathetensatz a2 = c · p 82 = 17 · p | : 17 p = 3,76 cm q = c – p = 17 – 3,76 = 13,24 cm h2 = p · q h2 = 3,76 · 13,24 | √ 7,06 cm |
||||||||||||||||||||||||||
|
||||||||||||||||||||||||||
| Ganz wichtig | ||||||||||||||||||||||||||
|
Den Höhensatz und die Kathetensätze kannst du wieder vergessen!
Naja, vielleicht nicht ganz. :O) Wenn du sie benötigst, schlägst du sie in der Formelsammlung nach. Auf jeden Fall haben sie längst nicht die Bedeutung des Pythagoras. Den auf keinen Fall vergessen!!! Pythagoras wirst du noch tausendmal brauchen!!! |
|
|||||||||||||||||||||||||