|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Mit dem Satz des Pythagoras kann man fehlende Seiten in rechtwinkligen Dreiecken berechnen. Wie vielfältig die Anwendungen hierzu sind, wirst du in dieser Lektion sehen.
|
 |
||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
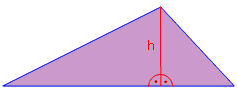
| Die Höhe in nicht-rechtwinkligen Dreiecken | |||||||||||||||||||||||||||||||
|
Pythagoras braucht rechtwinklige Dreiecke. Das heißt aber nicht, dass man bei anderen Dreiecken überhaupt nichts berechnen kann. Denn jedes Dreieck lässt sich über seine Höhe in zwei rechtwinklige Teildreiecke zerlegen.
|
|
||||||||||||||||||||||||||||||
|
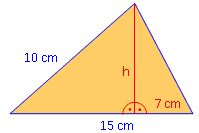
Beispiel 1:
Im Dreieck rechts soll die Höhe berechnet werden. Die Hypotenuse ist insgesamt 15 cm lang, der durch die Höhe abgetrennte rechte Teil davon 7 cm. Lösung: Der linke Teil der Hypotenuse ist: 15 – 7 = 8 cm lang. Damit kann man Pythagoras im linken Teildreieck anwenden: h2 = 102 – 82 h2 = 36 | √ h = 6 cm |
|||||||||||||||||||||||||||||||
|
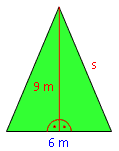
Beispiel 2:
Im nebenstehenden gleichschenkligen Dreieck ist die Basis 6 m lang, die Höhe 9 m. Berechne die Länge der beiden Schenkel s. Wir wenden Pythagoras im rechten oder linken Teildreieck an. Hier sind die Seitenlängen 9 m und 3 m (halbe Basis). s2 = 92 + 32 s2 = 90 | √ s = 9,49 m |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Diagonalen und Seiten in Vierecken | |||||||||||||||||||||||||||||||
|
Auch in Vierecken lassen sich viele rechtwinklige Teildreiecke finden, mit deren Hilfe man unbekannte Strecken berechnen kann.
|
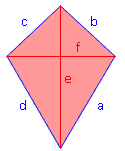
Über Pythagoras lassen sich für Vierecke aus den Diagonalen die Seitenlängen berechnen und umgekehrt.
|
||||||||||||||||||||||||||||||
|
Beispiel 3:
Ein Drachen besitze die Diagonalen e = 20 cm und f = 13 cm, wobei e durch f so geteilt wird, dass Teilstücke von 15 cm und 5 cm entstehen. Berechne die Seitenlängen der Diagonalen. Im Teildreieck oben rechts sind die Längen der beiden Katheten 6,5 cm (0,5·f) und 5 cm (kleines Teilstück von e). b2 = 6,52 + 52 b2 = 67,25 | √ b = 8,20 cm Im Teildreieck unten rechts sind die Längen der beiden Katheten 6,5 cm und 15 cm (großes Teilstück von e). a2 = 6,52 + 152 a2 = 167,25 | √ a = 16,35 cm |
|||||||||||||||||||||||||||||||
|
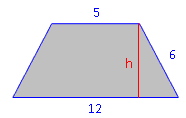
Beispiel 4:
Berechne die Höhe eines gleichschenkligen Trapezes mit den Grundlinien 12 und 5 cm und einer Schenkellänge von 6 cm. Wir rechnen im rechten Teildreieck. Dort haben wir bereits b, brauchen aber noch die untere Seite. Dieses Reststück ist die Hälfte von dem, was übrig bleibt, wenn man die obere von der unteren Grundlinie abzieht. x = 0,5 · (12 cm – 5 cm) = 0,5·7 cm = 3,5 cm h2 = 62 – 3,52 h2 = 23,75 | √ h = 4,87 cm |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Formeln für Höhen, Diagonalen etc. | |||||||||||||||||||||||||||||||
|
Statt konkret mit Zahlen können all diese Berechnungen auch mit Variablen/Buchstaben gemacht werden. Auf diese Weise erhält man dann Formeln, die für alle Probleme der entsprechenden Art verwendet werden können.
|
|
||||||||||||||||||||||||||||||
|
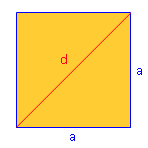
Beispiel 5:
Ermittle eine Formel für die Diagonale eines Quadrates in Abhängigkeit von der Seitenlänge a. (Auf Deutsch: Berechne die Diagonale d und nehme für die Seitenlänge statt einer Zahl den Buchstaben a. ;O) ) Im rechten Teildreieck gibt es die Katheten a und a sowie die Hypotenuse d. Also kann es losgehen: d2 = a2 + a2 d2 = 2a2 | √ d = √2a2 (aus a2 die Wurzel ziehen) d = √2 · a Und fertig ist die Formel. |
|||||||||||||||||||||||||||||||
|
Wenden wir unsere Formel doch einmal an: Wie groß ist die Diagonale eines Quadrates mit der Seitenlänge 25 cm?
d = √2 · 25 = 35,36 cm Das geht fix! |
|||||||||||||||||||||||||||||||
|
Beispiel 6:
Ermittle eine Formel für die Höhe eines gleichseitigen Dreiecks in Abhängigkeit von seiner Seitenlänge. Im rechten Teildreieck haben wir es mit den Seitenlängen h, a und
h = √
h =
|
|||||||||||||||||||||||||||||||
|
Formel anwenden: Wie hoch ist ein gleichseitige Dreieck mit der Seitenlänge 50 cm?
h =
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Die Länge von Vektoren und Strecken im Koordinatensystem | |||||||||||||||||||||||||||||||
|
Vektoren kennst du schon lange, aber noch nie hast du dich gefragt, wie lang ein bestimmter Vektor ist. Hätte aber eh nichts gebracht, weil man dazu den Satz des Pythagoras braucht.
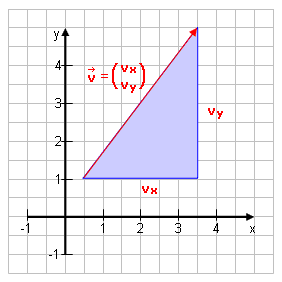
Zeichnet man zu einem Vektor
v2 = vx2 + vy2 | √ v = √vx2 + vy2 |
|
||||||||||||||||||||||||||||||
|
Beispiel 7:
Berechne die Länge des Vektors
v2 = 32 + (-5)2 v2 = 34 | √ v = 5,83 LE (Längeneinheiten) |
|||||||||||||||||||||||||||||||
|
Auf die gleiche Art berechnet man den Abstand zweier Punkte im Koordinatensystem. Oder, anders formuliert: die Länge der Strecke zwischen zwei Punkten.
Man bestimmt zunächst den Vektor zwischen den beiden Punkten (Spitze minus Fuß; Endpunkt minus Startpunkt) und errechnet dann die Länge des Vektors. |
|||||||||||||||||||||||||||||||
|
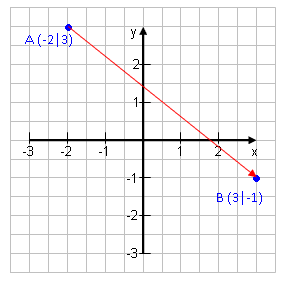
Beispiel 8:
Berechne den Abstand AB zwischen den beiden Punkten A(-2|3) und B(3|-1).Vektor:
Länge: AB = √52 + (-4)2 = √41 = 6,40 LE
|
|||||||||||||||||||||||||||||||