mathepanik.de

Lektion
Die Funktionsgleichung ermitteln

Worum geht es?

Die Geradengleichung wird uns leider nicht immer fertig auf dem Tablett serviert. Häufig müssen wir sie uns selbst erstellen.

Je nachdem, welche Informationen uns über die Gerade vorliegen, fallen die Berechnungen zum Ermitteln der Gleichung etwas unterschiedlich aus. Besonders schwer sind sie aber eigentlich nie.

In dieser Lektion lernst du:

	Die Geradengleichung zu ermitteln, wenn folgende Informationen gegeben sind:

1.	m und t

2.	m und ein Punkt

3.	t und ein Punkt

4.	zwei Punkte

5.	ein Punkt und eine parallele oder orthogonale Gerade

6.	Und zu testen, ob ein Punkt auf einer Geraden liegt.

Einführung

Wie du an der Auflistung erkennst, gibt es recht viele Varianten, die Geradengleichung zu berechnen. Sie sind alle nicht schwierig, aber es ist wichtig, dass du sie nicht auswendig lernst wie Vokabeln. Denn dann würdest du die Rechenwege leicht verwechseln.

Versuche lieber zu verstehen, welche prinzipiellen Gedanken man sich macht. Dann wirst du sehen, wie leicht das Rechnen funktioniert.

Geradengleichung bestimmen:

→ Suche nach m und t.
→ Einsetzen in y = m·x + t

Die Geradengleichung zu bestimmen bedeutet immer:
m und t herauszufinden!!!

Dann setzt man sie in y = m·x + t ein und ist fertig.

Alles, was du tun musst, ist m und t berechnen!

m und t gegeben

Naja! Um ehrlich zu sein, so eine leichte Fragestellung taucht nicht wirklich auf. Aber sie zeigt ganz gut, wie es funktioniert.

Gegeben sei eine Gerade g mit der Steigung -2, die bei 3,5 die y-Achse schneidet.

Hier gibt es nichts zu rechnen:
Steigung: m = -2
y-Achsenabschnitt: t = 3,5 → g: y = -2·x + 3,5

Einfach einsetzen, fertig!

m oder t und ein Punkt gegeben

Gegeben sei eine Gerade g mit der Steigung 0,5,
die durch den Punkt A(2|5) läuft.

Schon kniffliger!

y = m·x + t

Die Steigung ist bereits gegeben: m = 0,5
Also lautet die Gleichung: → y = 0,5·x + t

Fehlt nur noch t!!! Du brauchst immer m und t!

Der Trick: Immer wenn ein Punkt gegeben ist,
setzt du ihn für x und y ein!

Merke:

	Punkte immer für x und y einsetzen!!!

Achtung:

x und y beim Einsetzen nicht vertauschen!

A einsetzen: 5 = 0,5·2 + t

Nun t ausrechnen:

5 = 0,5·2 + t
5 = 1 + t | – 1
4 = t

Fertig! Gleichung: g: y = 0,5·x + 4

Zweites Beispiel:

Die Gerade g verlaufe durch B(3|-2) und schneide die y-Achse bei 4. Ermittle die Geradengleichung.

y = m·x + t t = 4 → y = m·x + 4

B einsetzen:

-2 = m·3 + 4 | – 4
-6 = m·3 | :3
-2 = m → g: y = -2·x + 4

Zwei Punkte gegeben

Hier müssen wir uns aus den beiden Punkten zunächst m ausrechnen. Dann läuft wieder alles wie gehabt.

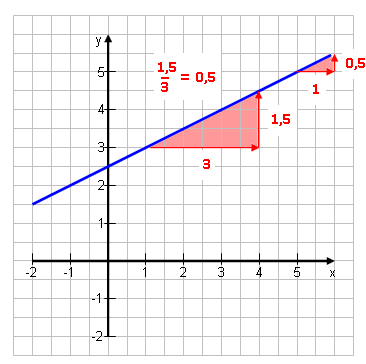
Gegeben sei eine Gerade g, die durch die beiden Punkte A(1|3) und B(4|4,5) läuft. Wie lautet die Geradengleichung?

Die Steigung m kann man folgendermaßen aus 2 Punkten berechnen:

m =

∆y

∆x

y₂ – y₁

x₂ – x₁

Dabei ist es egal, welchen Punkt man als ersten und welchen man als zweiten hernimmt.

Also: m =

4,5 – 3

4 – 1

1,5

= 0,5

→ y = 0,5·x + t

Es fehlt noch t: Einen (egal welchen!) der Punkte einsetzen:

3 = 0,5·1 + t | – 0,5
2,5 = t → g: y = 0,5·x + 2,5

Um von A nach B zu kommen, geht man 3 nach rechts (von 1 bis 4) und 1,5 nach oben (von 3 n. 4,5).

3 nach rechts, 1,5 nach oben, das ist das Gleiche wie 1 nach rechts und 0,5 nach oben! Die Steigung!

Merke:

Zwei Punkte gegeben:

m =

∆y

∆x

y₂ – y₁

x₂ – x₁

Zweites Beispiel:

Die Gerade g verlaufe durch P(-3|-4) und Q(2|5). Wie lautet die Geradengleichung?

y = m·x + t
m =

5 – (-4)

2 – (-3)

= 1,8

Q einsetzen:
5 = 1,8·2 + t | – 3,6
1,4 = t → g: y = 1,8·x + 1,4

Ein Punkt und eine parallele oder eine senkrechte Gerade

Die letzte der bekannten Varianten.

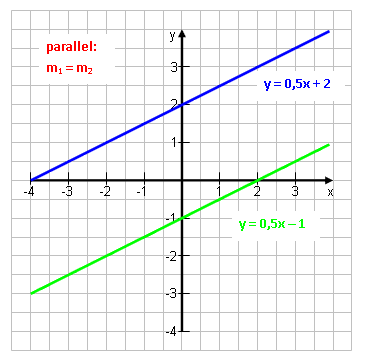
g verlaufe durch A(5|-2) und sei parallel zur Geraden h: y = 3·x – 5. Wie lautet die Gleichung von g?

Nun, was hier ein wenig verschlüsselt angegeben wird, ist nichts anderes als die Steigung m. Wenn g parallel zu h ist, hat es die gleiche Steigung! Hier also 3.

m einsetzen, A einsetzen, ausrechnen, fertig!

y = 3·x + t
-2 = 3·5 + t | – 15
-17 = t → g: y = 3·x – 17

Merke:

parallele Gerade:
m₁ = m₂

senkrechte Gerade:
m₁ =

–

m₂

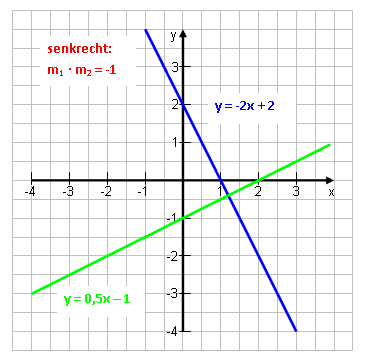
g verlaufe durch A(5|-2) und sei senkrecht (orthogonal) zur Geraden h: y = 3·x – 5. Wie lautet die Gleichung von g?

Auch hier ist die Steigung von m verschlüsselt gegeben!

Wenn eine Gerade senkrecht auf einer anderen steht, dann gilt für ihre Steigungen m₁ und m₂:

m₁ · m₂ = –1

3 und

stehen senkrecht aufeinander.
Oder 2 und -0,5. Oder -10 und 0,1 etc.

Soll man die eine Steigung aus der anderen berechnen:

m₁ =

–

m₂

Beispiel: m₂ = 4 → m₁ = -

–

= -0,25

Bei uns war die Steigung m₂ der zweiten Geraden 3.

Also: m₁ = -

A einsetzen:
-2 = -

·5 + t | +

= t → g: y =

x –

Punkte testen

Manchmal soll man testen, ob ein bestimmter Punkt auf der Geraden liegt.

Gegeben sei g: y = 3x – 4
Teste ob P (2|-7) auf g liegt.

Super einfach! Die x-Koordinate in die Gleichung einsetzen und nachrechnen, ob wirklich die y-Koordinate des Punktes herauskommt.

-7 = 3·2 – 4 ?
-7 = 2 falsche Aussage! P liegt nicht auf g.

Arbeiten mit der Punkt-Steigungs-Form

y = m·(x – x_P) + y_P

In der Punkt-Steigungs-Form gibt es kein t, sondern nur m und die Koordinaten eines Punktes. Von daher ist sie gut zum rechnen geeignet, wenn m und ein Punkt gegeben sind. Halbwegs auch noch bei zwei Punkten.

Es gibt Lehrer, die sind Fans der Punkt-Steigungs-Form.

Schwer zu sagen, ob es sich wirklich lohnt, diesen zweiten Rechenweg zu lernen.

m und ein Punkt gegeben

g laufe durch A(5|-2) und besitze die Steigung 3.

Lsg: A für x_p/y_p einsetzen

y = 3 · (x – 5) + (-2)
= 3·x – 15 – 2
= 3·x – 17

zwei Punkte gegeben

g laufe durch A(3|-1) und B(-3|2).

Lsg: A für x_p/y_p und B für x/y einsetzen

2 = m·(-3 – 3) + (-1)
2 = m·(-6) – 1  | + 1  : (-6)
-0,5 = m

y = -0,5·(x – 3) – 1
  = -0,5·x + 1,5 – 1
  = -0,5x + 0,5

Fehler gefunden oder Anregungen?