|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Wenn ein Klimaforscher berechnet, wie schnell sich wegen des Treibhauseffektes die Erde erwärmt, wenn der Formel-I Ingenieur berechnet, für wie viele Runden der getankte Treibstoff noch reicht, wenn der Sozialwissenschaftler berechnet, wie hoch der Anteil an unter 18 Jährigen in 5 Jahren sein wird – in all diesen Fällen werden Formeln verwendet, um die gewünschte Größe auszurechnen. |

Wie kommt die Sonde zum Mars? Hunderte von Formeln benötigen die Wissenschaftler, um die richtige Startgeschwindigkeit zu berechnen, die korrekte Bahn, den geeigneten Moment zum abbremsen und die Stärke der Bremskraft. Ein Fehler und 300 Millionen Euro sind futsch.
|
||||||||||||||||||||||||||||||
|
Terme sind nichts anderes als eben solche Formeln. Du kannst etwas einsetzen, z.B. wie viel Treibstoff getankt wurde und es kommt etwas heraus, z.B. für wie viele Runden er noch reicht.
|
|||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Wozu man Terme braucht | |||||||||||||||||||||||||||||||
|
Kaum ein Schüler kann beantworten, wozu man Terme braucht. Fragt man aber, wozu man Formeln braucht, gibt es jede Menge Antworten. Oben haben wir einige Beispiele beschrieben. Unzählige weitere kannst du dir selbst ausmalen: Immer wenn irgendetwas berechnet werden soll, verwendet man eine Formel.
|
Terme sind Formeln!
Die Mathematiker sind Künstler im Verschleiern allzu einfacher Tatsachen.
Ohne Variable macht eine Formel keinen Sinn.
Komplizierte Formeln besitzen sogar mehrere Variablen. Die Formel zur Erderwärmung braucht sicherlich zehn verschiedene Variablen, vielleicht sogar noch mehr.
|
||||||||||||||||||||||||||||||
|
Und ein Term ist nichts anderes als eine Formel.
Einfach nur ein anderes Wort für Formel!!! |
|||||||||||||||||||||||||||||||
|
Formeln brauchen Variablen! Warum? Damit man unterschiedliche Zahlen einsetzen kann!
|
|||||||||||||||||||||||||||||||
|
Nehmen wir an, du dürftest nach London reisen. Flug und Besichtigungsprogramm kosten zusammen 190,- €, Übernachtung und Verpflegung pro Tag 40,- €.
Was kostet dein Urlaub? Das hängt natürlich von der Anzahl der Übernachtungen ab!!! 190 + x · 40 x ist die Anzahl der Übernachtungen. Für x kannst du eine unterschiedliche Anzahl von Tagen einsetzen. |
|||||||||||||||||||||||||||||||
|
Benennung:
Jedes Ding will einen Namen. Terme bekommen meistens den unglaublich phantasievollen Namen T. Außerdem gibt man gerne in Klammern an, wie ihre Variable heißt: T(x). Also: T(x) = 190 + x · 40 |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Einsetzungen und Termwerte | |||||||||||||||||||||||||||||||
|
Jede Formel bringt unterschiedliche Ergebnisse, je nachdem, welche Zahl man für die Variable einsetzt.
Die Formel 3x + 7 liefert eine 13, wenn ich 2 für x einsetze und eine 22, wenn ich 5 für x einsetze. Man schreibt: x = 2 → T(x) = 13 x = 5 → T(x) = 22 Oder man schreibt die Zahl, die man eingesetzt hat einfach in Klammern: T(2) = 13 T(5) = 22 Das, was bei einer bestimmten Einsetzung heraus kommt, nennt man den Wert des Terms. Oder kurz: den Termwert. |

|
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Die Wertetabelle | |||||||||||||||||||||||||||||||
|
Möchte man gleich für mehrere Einsetzungen die Werte der Formel berechnen, erstellt man lieber eine Tabelle, als alle Werte einzeln aufzuschreiben.
In der Wertetabelle schreibt man oben die Einsetzungen hin, darunter jeweils das, was raus kommt. |
So eine Wertetabelle sieht nach nicht viel aus, aber oft steckt viel Arbeit dahinter, bis man alle Werte berechnet hat.

|
||||||||||||||||||||||||||||||
|
T(x) = 3x + 7
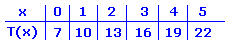
|
|||||||||||||||||||||||||||||||
|
Die eingesetzten Zahlen für x sind oft auch negativ. Denke nur an Formeln im Finanzwesen. Da sind negative Zahlen (Schulden) etwas ganz natürliches.
|
|||||||||||||||||||||||||||||||
|
T(x) = 0,5x + 4
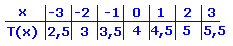
|
|||||||||||||||||||||||||||||||
|
Welche Zahlen man einsetzen soll, wird bei der Aufgabenstellung angegeben. Dazu gibt es viele Möglichkeiten:
G = {-3; -2; -1; 0; 1; 2; 3} oder x ϵ {-3; ...; 3} oder x ϵ [-3; 3] usw. |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Graphische Auswertung | |||||||||||||||||||||||||||||||
|
Stell dir vor, der Wert einer Aktie für alle Tage des letzten Jahres würde als Wertetabelle angezeigt. HILFE! Oder der Anteil der unter 18 Jährigen für die nächsten 20 Jahre. Oh nein!
|

|
||||||||||||||||||||||||||||||
|
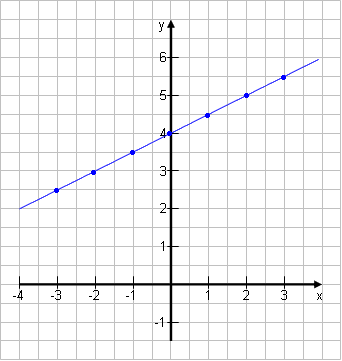
Zu viele Zahlen auf einmal verkraftet niemand. Für solche Fälle zeigt man die Werte einer Formel besser in graphischer Form.
Die eingesetzten x-Werte werden nach rechts oder links dargestellt (in x-Richtung). Die Termwerte, die herauskommen, nach oben oder unten (in y-Richtung). |
|||||||||||||||||||||||||||||||
|
Beispiel:
T(x) = 0,5x + 4 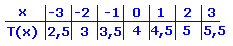 |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
|
Noch ein Beispiel:
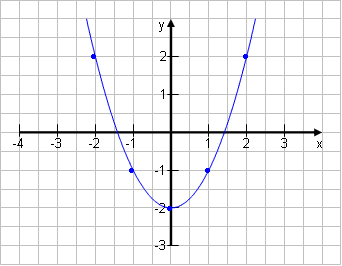
T(x) = x² -2 x ϵ [-2; 2] 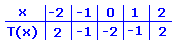 NR: (-2)2 – 2 = 2 (-1)2 – 2 = - 1 .....
Manche Lehrer verlangen Kreuzchen, manche verlangen Punkte. Manche verlangen Pfeile von der x-Achse bis zum y-Wert. Meistens werden die Punkte verbunden.
|
|
||||||||||||||||||||||||||||||







