|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||
|
Terme (Formeln) wie x2 + 2x + 1 oder 3x2 – 4x + 2 heißen quadratische Terme. Sie werden in der zehnten Klasse und in der Abschlussprüfung eine Hauptrolle spielen. Deshalb bereitet man sie in der achten Klasse bereits ein wenig vor.
Quadratische Terme ergeben sich in der Praxis recht häufig, wenn man interessante Größen berechnen will. Das besondere an ihnen ist, dass sie einen Extremwert besitzen. Es gibt eine Zahl, die man für x einsetzen kann, bei der die Formel den größten (oder kleinsten Wert) liefert. |
 |
||||||||||||||||||||||||

|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Quadratische Terme | |||||||||||||||||||||||||
|
Quadratische Terme sind solche Terme, deren höchste x-Potenz ein x2 ist.
Außer dem x2 kann der Term auch gerne noch x-en oder Zahlen enthalten, aber eben kein x3 oder x4 usw.
Beispiele: y = x2 y = 2x2 + 4 y = -x2 + x y = 2x2 – 3x + 1 |
Quadratische Terme
haben x2 als höchste x-Potenz. |
||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Wertetabelle und Graph | |||||||||||||||||||||||||
|
Die Wertetabellen zeichnen sich dadurch aus, dass die y-Werte zuerst steigen um dann wieder zu fallen. Oder umgekehrt: Zuerst fallen sie, dann steigen sie wieder.
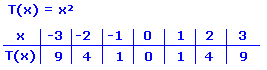
|
Die Graphen heißen Parabel. Sie haben eine typische Form. Fallen zuerst und steigen dann wieder, oder umgekehrt. Deutlich ist der Extremwert zu sehen. Manchmal ist es ein Minimum, manchmal ein Maximum.
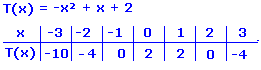 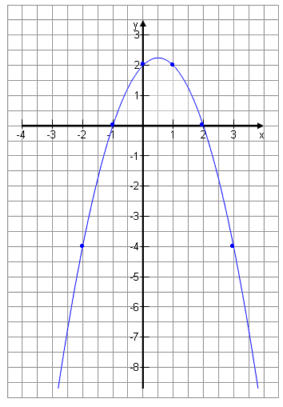 |
||||||||||||||||||||||||
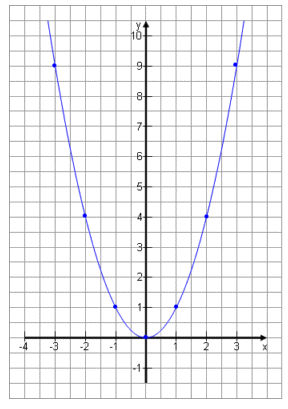
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Die Eigenschaften einer Parabel | |||||||||||||||||||||||||
|
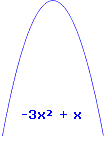
Wie du siehst, kann eine Parabel nach oben geöffnet sein oder nach unten. Ob der erste oder der zweite Fall vorliegt, kann man bereits an dem Term ablesen:
Ist die Zahl vor dem x2 positiv, so ist die Parabel nach oben geöffnet, ist sie negativ, dann ist die Parabel nach unten geöffnet. y = 2x2 + 4x nach oben geöffnet y = -3x2 + x nach unten geöffnet |

|
||||||||||||||||||||||||
|
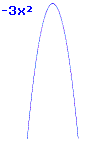
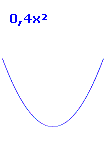
Einige Parabeln sind steil (eng), andere flach (gestaucht). Auch diese Eigenschaft kann man direkt am Term ablesen. Steht eine vom Betrag her große Zahl (> 1) vor dem x, dann geht es steil nach oben oder unten. Ist die Zahl eher klein (< 1), dann ist die Parabel flach.
y = -3x2 – 2x nach unten geöffnet, sehr steil y = 0,4x2 + 3 nach oben offen, ziemlich flach |
|||||||||||||||||||||||||
|
Was einen aber am meisten an einer Parabel interessiert, ist der Scheitelpunkt. Also der kleinste oder der größte Wert – je nachdem ob die Parabel nach oben oder unten geöffnet ist.
Diesen Wert kann man meistens leider nicht am Term ablesen. Mit etwas Glück erkennt man ihn in der Wertetabelle. Im ersten Beispiel oben, y = x2 sieht man in der Wertetabelle, dass die Parabel ihr Minimum bei x = 0 hat. Ihr Wert ist dort 0. Im zweiten Beispiel, y = -x2 + x + 2 kann man anhand der Wertetabelle erahnen, dass sie ihr Maximum bei x = 0,5 hat. Den Wert bekommen wir heraus, wenn wir 0,5 für x einsetzen: T(0,5) = -0,52 + 0,5 + 2 = 2,25. In den meisten Fällen hilft aber auch die Wertetabelle nicht weiter. |
|||||||||||||||||||||||||
|
Wie wir in der nächsten Lektion sehen werden, gibt es jedoch ein Rechenverfahren, das es uns erlaubt, diesen Extremwert zu berechnen, ohne dass man eine Wertetabelle erstellen oder den Graphen zeichnen müsste.
|
|||||||||||||||||||||||||







