|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||
|
Wenn eine Gerade von einer anderen Geraden geschnitten wird, bilden sich 4 Winkel. Sind sie alle beliebig und verschieden, oder haben sie etwas miteinander zu tun?
Wenn zwei parallele Geraden von einer anderen geschnitten werden, bilden sich an jedem der beiden Schnittpunkte 4 Winkel. Wie ist es mit diesen 8 Winkeln? |
 |
||||||||||||||||||||||||

|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Scheitelwinkel und Nebenwinkel | |||||||||||||||||||||||||
|
Wenn eine Gerade von einer anderen Geraden geschnitten wird, bilden sich 4 Winkel. Und du siehst sofort, dass sie nicht alle verschieden sind.
|
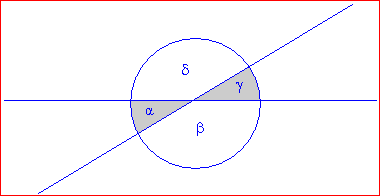
Merke:
Scheitelwinkel sind immer gleich groß. Zwei Nebenwinkel ergeben zusammen 180°. |
||||||||||||||||||||||||
|
Zwei sich gegenüber liegende Winkel – man nennt sie Scheitelwinkel – sind immer gleich groß.
α = γ und β = δ |
|||||||||||||||||||||||||
|
Zwei Winkel, die nebeneinander liegen – man nennt sie Nebenwinkel – ergänzen sich immer zu einer kompletten Geraden, also zu 180°.
α + β = 180° ; β + γ = 180° γ + δ = 180° ; δ + α = 180° |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Stufenwinkel und Wechselwinkel (Z-Winkel ) | |||||||||||||||||||||||||
|
Nun schauen wir uns die Situation an, die entsteht wenn zwei parallele Geraden von einer anderen Geraden geschnitten werden.
Hier entstehen an jedem der beiden Schnittpunkte wieder 4 Winkel, für deren Scheitel- und Nebenwinkel wieder das oben Gesagte gilt. Da zwei der Geraden parallel sind, kann man aber auch die Winkel an verschiedenen Schnittpunkten miteinander vergleichen: |
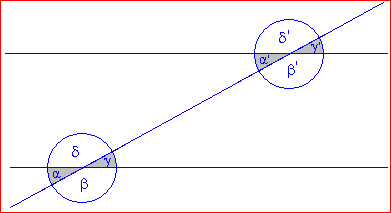
Merke:
Stufenwinkel sind immer gleich groß. Wechselwinkel (Z-Winkel) 
|
||||||||||||||||||||||||
|
α ist genau der gleiche Winkel wie α', nur dass α' eine Stufe höher liegt. Man nennt die beiden deshalb "Stufenwinkel".
Das Gleiche gilt natürlich auch für β und β' usw. Stufenwinkel sind also immer gleich groß! |
|||||||||||||||||||||||||
|
Und wie ist es, wenn man γ und α' miteinander vergleicht?
Auch die sind gleich groß, denn γ ist ja genauso groß wie γ' (nur eine andere Stufe) und γ' und α' liegen sich ja direkt gegenüber (Scheitelwinkel). Um von γ zu α' zu gelangen, muss man nur einmal schräg die Seite wechseln, deshalb nennt man sie Wechselwinkel. Viele sagen auch Z-Winkel, weil sich eine Art Z ergibt. Wechselwinkel (Z-Winkel) sind also ebenfalls immer gleich groß. |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Mit Winkeln rechnen | |||||||||||||||||||||||||
|
Nachdem du weißt, wie sich die Winkel an den Schnittpunkten verhalten, kannst du unbekannte Winkel leicht ausrechnen.
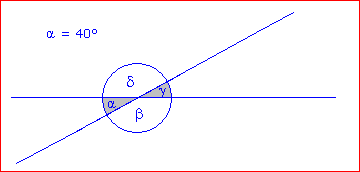
Aufgabe 1: α = 40°. Berechne β, γ und δ. |
|
||||||||||||||||||||||||
|
Lösung:
γ ist genauso groß wie α (Scheitelwinkel), also: γ = 40° β ist der Nebenwinkel zu α, also: β = 180° – 40° = 140° δ ist wieder genauso groß wie β, also: δ = 140° |
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
|
Aufgabe 2:
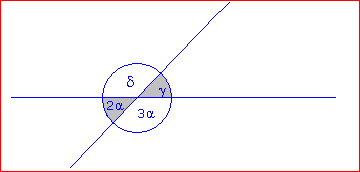
Berechne α, β, γ und δ. |
|
||||||||||||||||||||||||
|
Lösung:
2α und 3α sind Nebenwinkel, also ergeben sie zusammen 180°: 2α + 3α = 180°. 5α = 180° | : 5 α = 36° γ = 2α = 2·36° = 72° δ = 3α = 3·36° = 108° |
|||||||||||||||||||||||||







