|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Für viele technische Probleme braucht man das Koordinatensystem. Ohne ein Koordinatensystem wird heute kein Haus mehr geplant, kein Möbel designed, keine Wettervorhersage berechnet und kein Flugzeug mehr gelandet.
|
 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Orte, die man in seinen Plan einträgt (Eckpunkte des Hauses, Positionen des Flugzeugs etc.), sind dann Punkte im Koordinatensystem.
Bewegungen der Wolken und Verschiebungen des Flugzeugs werden als Pfeile eingetragen: als Vektoren und Parallelverschiebungen. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

|
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Das Koordinatensystem | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
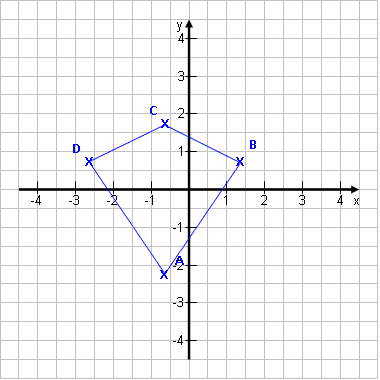
Wir haben inzwischen auch negative Zahlen und Kommazahlen kennengelernt. Für unser früheres Gitternetz bedeutet das, dass wir links von der Null und unterhalb von ihr nun ebenfalls Punkte eintragen können. Und dass die Punkte nicht nur genau auf den Gitterkreuzen liegen dürfen, sondern auch dazwischen.
Statt Gitterkreuz nennen wir es nun Koordinatensystem. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

Merke:
Ein Koordinatensystem braucht: Pfeilspitzen nach rechts und nach oben! (KEINE nach links und nach unten!!!) Ein x an die rechte Pfeilspitze und ein y an die obere! Mindestens EINE Zahl an jeder Achse, damit man weiß, welche Skalierung benutzt wird, also welche Bedeutung ein Kästchen oder 1 cm hat. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
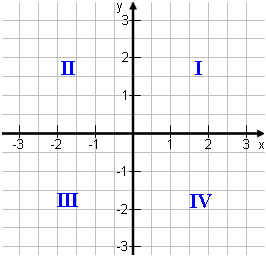
Quadranten
Die vier Viertel des Koordinatensystems nennt man Quadranten. Man zählt sie von eins bis vier durch und nimmt die römischen Zahlen. Oben rechts, also das frühere Gitternetz, ist Quadrant I. Dann geht es gegen den Uhrzeigersinn weiter mit den Quadranten II, III und IV. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Punkte im Koordinatensystem | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Punkte werden mit Großbuchstaben
bezeichnet: A B C ... Jeder Punkt erhält in Klammern seine x- und seine y-Koordinate: A (1,5 | 3,5) ; B (-2,5 | -1) Zuerst kommt die x- dann die y-Koordinate. Genau wie im Alphabet, zuerst x dann y. Beim Einzeichnen: Die x-Koordinate nach rechts (oder links, wenn negativ). Die y-Koordinate nach oben (oder unten, wenn negativ). Zuerst also nach rechts, dann erst nach oben! |
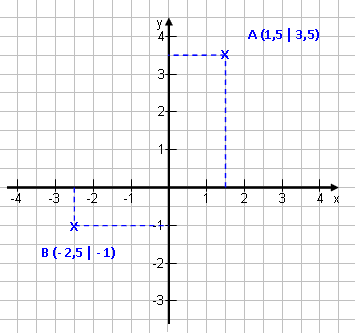
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Vektoren: Ein Punkt auf Wanderschaft | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Soll ein Punkt verschoben werden, muss man angeben, um wie viel er in x-Richtung (nach rechts oder links) und um wie viel er in y-Richtung (nach oben oder unten) verschoben werden soll.
Eine solche Verschiebung nennt man Vektor. |
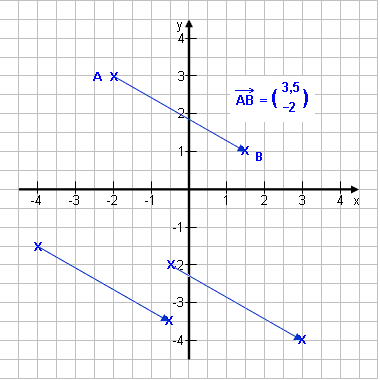
Weil ein Vektor nur noch die Verschiebungen enthält, jedoch nicht mehr seinen Ausgangspunkt, kann man ihn auch auf andere Punkte anwenden.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Vektoren bezeichnet man entweder mit Kleinbuchstaben oder mit Anfangs- und Endpunkt. Außerdem zeichnet man einen kleinen Pfeil darüber:
Die Verschiebungen schreibt man in runden Klammern übereinander. Zuerst die in x-Richtung, dann die in y-Richtung:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Beispiele:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Parallelverschiebung: Möbelrücken | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
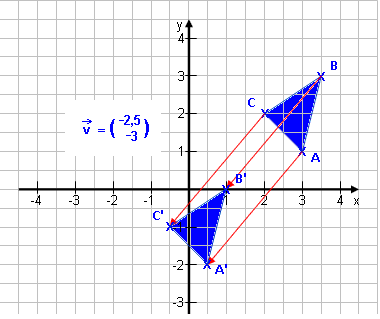
Eine Parallelverschiebung ist das Verschieben von mehreren Punkten um den gleichen Vektor. Weil es jedes Mal die gleiche Verschiebung ist, wird nichts verdreht oder in seiner Form verändert, sondern einfach nur parallel verschoben. Wie wenn du im Sommer auf einer Decke liegst und diese in den Schatten ziehen willst. Wenn du die eine Ecke um 2 m nach links und 1 m nach oben verschiebst, machst du das anschließend genauso auch für alle anderen drei Ecken. |
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||







