Lektion
   Rechnen mit Vektoren I   
Hilfe
Diskutieren
Panik-Test
Themenübersicht
zu den Übungsaufgaben
Worum geht es?
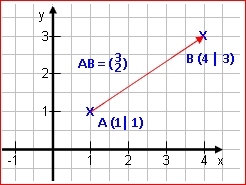
Vektoren zu zeichnen macht zwar Spaß, ist manchmal aber auch etwas mühsam.

Um herauszufinden, wo ein Punkt landet, nachdem man ihn verschoben hat, muss nicht wirklich gezeichnet werden: So etwas kann man berechnen.

Oder wo er vorher lag, wenn man weiß, wo er landet. Oder um wie viel er verschoben wurde, wenn man Anfangs- und Zielpunkt kennt.

Wie solche Rechnungen funktionieren, erfährst du in dieser Lektion.
 

         
In dieser Lektion lernst du
1.Den Zielpunkt zu berechnen.
2.Den Startpunkt zu berechnen.
3.Die Koordinaten eines Vektors zu berechnen.
4.Was der Gegenvektor und was ein Ortsvektor ist.
  




Vorüberlegungen
Stell dir vor, du hast ein Messband auf dem Boden liegen mit Markierungen für jeden Meter: 1, 2, 3 ...

Wir starten bei einem Startpunkt, gehen eine bestimmte Strecke und kommen an einem Zielpunkt an.
 







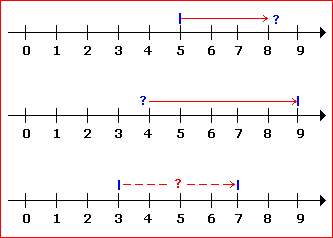
Zielpunkt berechnen:

Du startest bei Marke 5 und gehst 3 Meter. Wo landest du?

5 + 3 = 8.  Startpunkt plus Vektor!


Startpunkt berechnen:

Du kommst bei 9 an und bist 5 Meter gegangen. Wo bist du gestartet?

9 – 5 = 4.  Zielpunkt minus Vektor!


Vektor berechnen:

Du startest bei 3 und du kommst bei 7 an. Wie weit bist du gegangen?

7 – 3 = 4.  Zielpunkt minus Startpunkt.
 
Lächerlich einfach, nicht wahr?

Nun Alles noch einmal ganz langsam und für die beiden Dimensionen des Vektors:
 
Den Zielpunkt berechnen
Der Punkt A(2 | 4) soll um den Vektor 
→
AA'
 
 =  (
1
3
 )
verschoben werden. Berechne den Zielpunkt A'.

Einfach zu den Koordinaten des Punktes die Koordinaten des Vektors addieren und du erhältst den Zielpunkt:

A': A' (2 + 1 | 4 + 3) = A' (3 | 7)
 




Zielpunkt = 

    Startpunkt + Vektor
Beispiele:
P (3 | 5) ; 
→
PP'
 
 =  (
2
5
 )
 Berechne P'.
P': P' (3 + 2 | 5 + 5) = P' (5 | 10)

A (-2 | -1,5) ; 
→
AB
 
 =  (
6
-3
 )
 Berechne B.
B: B (-2 + 6 | -1,5 + (-3)) = B (4 | -4,5)
 
Den Startpunkt berechnen
Der Punkt A' (5 | 3) wurde um den Vektor 
→
AA'
 
 =  (
4
3
 )
verschoben. Berechne den Startpunkt A.

Einfach von den Koordinaten des Zielpunktes die Koordinaten des Vektors abziehen und du erhältst den Startpunkt:

A: A (5 – 4 | 3 – 3) = A (1 | 0)
 

Startpunkt = 

    Zielpunkt – Vektor




Beispiele:
C' (6 | 2) ; 
→
CC'
 
 =  (
3
4
 )
 Berechne C.
C: C (6 – 3 | 2 – 4) = C (3 | -2)

Q (-3 | 6,5) ; 
→
PQ
 
 =  (
-2
1
 )
 Berechne P.
P: P (-3 – (-2) | 6,5 – 1) = P (-1 | 5,5)
 
Den Vektor berechnen
Der Punkt A (1 | 2) wurde auf den Punkt A' (5 | 4) verschoben. Berechne den Vektor 
→
AA'
 
.

Einfach die Koordinaten des Zielpunktes minus die des Startpunktes rechnen und du erhältst den Vektor:

→
AA'
 
 =  (
5 – 1
4 – 2
 ) =  (
4
2
 )
  




Vektor = 

    Zielpunkt – Startpunkt
(Spitze minus Fuß)
Beispiele:
E (6 | 4) ; F (3 | 7) Berechne 
→
EF
 
.

→
EF
 
 =  (
3 – 6
7 – 4
 ) =  (
-3
3
 )
 

P (-2 | -5) ; P' (4 | -5) Berechne 
→
PP'
 
.

→
PP'
 
 =  (
4 – (-2)
-5 – (-5)
 ) =  (
6
0
 )
  
Der Gegenvektor
Hat man einen Punkt mit einem Vektor verschoben, könnte man ihn mit dem Gegenvektor wieder zurück verschieben.

Statt 4 nach rechts würde man nun 4 nach links zurück verschieben. Statt 5 nach oben nun 5 nach unten.

Der Gegenvektor ist also exakt die umgekehrte Verschiebung.
 

Gegenvektor:

Einfach die Vorzeichen umkehren.




Um zu einem Vektor den Gegenvektor zu berechnen, drehst du deshalb einfach die Vorzeichen um:

→
AB
 
 =  (
4
5
 ) → 
→
BA
 
 =  (
-4
-5
 )
 

→
PP'
 
 =  (
0,5
-3
 ) → 
→
P'P
 
 =  (
-0,5
3
 )
 

→
v
 
 =  (
0
7
 ) → 
→
v*
 
 =  (
0
-7
 )
  
Der Ortsvektor
Der Ortsvektor ist der große Langweiler unter den Vektoren: Er besagt einfach, wie man vom Ursprung zu einem Punkt gelangt.

Jeder Punkt besitzt deshalb seinen eigenen Ortsvektor und dieser hat exakt die gleichen Koordinaten wie der Punkt selbst.
 
P (3 | 7)  →  
→
OP
 
 =  (
3
7
 )
 

Q (-6 | -0,5)  →  
→
OQ
 
 =  (
-6
-0,5
 )
  

Fehler gefunden oder Anregungen?