|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Formeln benötigt man um die unterschiedlichsten Größen zu berechnen.
13 · x + 170 Die Formeln haben Variablen (z.B. x), in die kann man Zahlen einsetzen und erhält dann unterschiedliche Ergebnisse. Oft ist es nun so, dass das Ergebnis feststeht, man aber wissen möchte, welche Zahl (welches x) man einsetzen muss, damit dieses Ergebnis herauskommt. 13 · x + 170 = 400 x = ??? So ergibt sich eine Gleichung. Man kennt das Ergebnis und will das richtige x herauskriegen. |
Gleichungen sind Rätsel. Ich sage dir, was rauskommt, sag du mir, was man dazu eingesetzt hat.
|
||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Einfache Gleichungen lösen | |||||||||||||||||||||||||||||||
|
Eine Gleichung zu lösen heißt, sie so umzuformen, dass man am Ende auf x kommt: x = .....
Dazu muss man auf beiden Seiten die gleiche Umformung durchführen. Wie wenn ein Händler früher mit einer Waage den Inhalt eines verschlossenen Beutels herausfinden wollte. Er hat auf beiden Seiten die gleiche Anzahl an Münzen weggenommen, hinzugefügt, er hat die Anzahl der Beutel und der Münzen halbiert, verdoppelt etc. Aber immer das Gleiche auf beiden Seiten! |
Wahnsinnig schwierig, was? ;O)
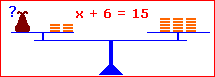 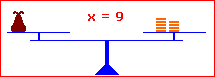 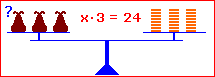 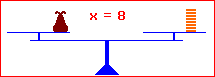

|
||||||||||||||||||||||||||||||
|
Die vier einfachsten Umformungen
x + 6 = 15 | – 6 x = 9 L = {9} x – 7 = 18 | + 7 x = 25 L = {25} x · 3 = 24 | : 3 x = 8 L = {8} x : 6 = 7 | · 6 x = 42 L = {42} Die Rechnung, die man durchführt, schreibt man mit einem Kommandostrich hinter die Gleichung. Am Ende beantwortet man die Frage nach dem richtigen x, indem man eine Lösungsmenge angibt. |
|||||||||||||||||||||||||||||||
|
Wie du siehst, musst du immer die Gegenoperation durchführen. Steht in der Gleichung x + 6, so musst du – 6 rechnen, um die 6 zu entfernen. Genauso wie der Händler mit der Waage.
|
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Die Reihenfolge der Umformungen | |||||||||||||||||||||||||||||||
|
Nun sind Formeln aber oft nicht so einfach wie gerade gezeigt. Deshalb braucht man meistens mehrere Umformungsschritte, bis man x heraus bekommt.
|
Immer
zuerst Plus und Minus, dann erst Mal und Geteilt!!! 
|
||||||||||||||||||||||||||||||
|
3 · x + 7 = 22 | – 7
3 · x = 15 | : 3 x = 5 L = {5} Auch nicht schwer! Die einzige Schwierigkeit besteht darin, sich die richtige Reihenfolge zu merken: Zuerst Plus und Minus, dann erst Mal und Geteilt! |
|||||||||||||||||||||||||||||||
|
Warum eigentlich? Die Formel "verpackt" das x zwei mal: Zuerst wird das x mit 3 malgenommen, dann wird 7 addiert, weil ja Punktrechnen vor Strichrechnen geht. Beim "Auspacken" müssen wir logischerweise anders herum vorgehen: Wir machen zunächst die + 7 durch – 7 rückgängig. Und anschließend das · 3 durch : 3.
|
|||||||||||||||||||||||||||||||
|
Beispiele:
4x – 7 = 19 | + 7 4x = 26 | : 4 x = 6,5 L = {6,5} 6 + 2x = 34 | – 6 2x = 28 | : 2 x = 14 L = {14} x : 6 – 12 = -7 | + 12 x : 6 = 5 | · 6 x = 30 L = {30} |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Zuerst vereinfachen, dann umformen | |||||||||||||||||||||||||||||||
|
Häufig sind die Terme, die in einer Gleichung stehen, unnötig kompliziert. Solche Gleichungen löst man nicht sofort, da es bei den Umformungen viel zu leicht zu Fehlern kommen kann. Nein: Solche Gleichungen werden zuerst vereinfacht, dann erst gelöst!
2x – 4 + 3x + 2 = 53 (zuerst vereinfachen) 5x – 2 = 53 | + 2 5x = 55 | : 5 x = 11 L = {11} |

Die Division ganz zum Schluss muss man nicht wirklich ausrechnen. Es reicht, dass man sie als Bruch hinschreibt. Das spart viel Arbeit! Allerdings muss der Bruch vollständig gekürzt sein.
|
||||||||||||||||||||||||||||||
|
Beispiele:
-13x + 45 + 6x – 17 = 84 -7x + 28 = 84 | – 28 -7x = 56 | : (-7) x = -8 L = {-8} 8x + 5 – 9 + 13x = 23 – 8 21x – 4 = 15 | + 4 21x = 19 | : 21 x =
|
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Ungewöhnliche Lösungen | |||||||||||||||||||||||||||||||
|
Es gibt zwei Situationen, die zu einer recht ungewöhnlichen Lösung führen.
1. Leere Menge 4x + 6 – 4x +1 = 13 (vereinfachen) 7 = 13 Die x-en sind vollständig weggefallen. 4x – 4x ergibt 0x und die schreibt man erst gar nicht hin. Denn du prahlst ja auch nicht bei Freunden mit den Sachen die du nicht hast: 0 Pferde, 0 Ferraris und 0 Millionen. :O) Nun gibt es diese seltsame Situation: 7 = 13 Und es stellt sich die Frage: Welche Zahl kann ich für x einsetzen, damit 7 gleich 13 ist? Antwort: Keine! 7 ist nie 13. Es gibt kein x, das unsere Gleichung löst! Deshalb ist die Lösungsmenge leer: L = {} |
Leere Menge:
L={} oder L = ∅
Alle Zahlen:
L = Q 
|
||||||||||||||||||||||||||||||
|
2. Alle Zahlen
9x – 3 + 2x + 12 – 11x = 9 (vereinfachen) 9 = 9 Wieder sind alle x-en weggefallen. 9 = 9. Welche Zahl kann ich für x einsetzen, damit 9 gleich 9 ist? Alle! 9 ist immer gleich 9. Alle Zahlen lösen unsere Gleichung. Alle Zahlen, also die Menge Q: L = Q |
|||||||||||||||||||||||||||||||
|
Beispiele: 4x – 8 – 4x = 9 -8 = 9 L = {} 6x + 12 – 6x = 12 12 = 12 L = Q |
|||||||||||||||||||||||||||||||