|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||
|
Der Thaleskreis ist eine geometrische Konstruktion, die eine wirkliche Überraschung bietet. Mehr soll hier zunächst nicht verraten werden.
Was eine Tangente ist, weiß jeder. Aber, wie zeichnet man eigentlich von einem weit außerhalb gelegenen Punkt eine genaue Tangente an einen Kreis? Um dies und einiges mehr geht es in dieser Lektion. |
 |
||||||||||||||||||||||||

|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Der Thaleskreis | |||||||||||||||||||||||||
|
Wir gehen von einer Strecke [AB] aus.
 Wenn wir irgendeinen dritten Punkt C hinzunehmen, können wir aus den drei Punkten ein Dreieck formen. Der Winkel γ (Gamma) am Punkt C ist natürlich umso größer, je näher C an der Strecke [AB] ist, da dann das Dreieck immer flacher wird. Und er ist umso kleiner, je weiter weg der Punkt C liegt, da das Dreieck dann immer spitzer wird. 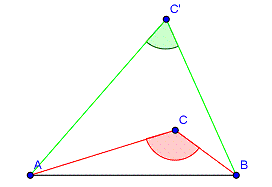
|
|
||||||||||||||||||||||||
|
Da man in der Technik besonders an rechtwinkligen Dreiecken interessiert ist, stellt man sich die Frage, wo genau eigentlich C liegen muss, damit sich bei γ ein rechter Winkel ergibt, man also ein rechtwinkliges Dreieck erhält.
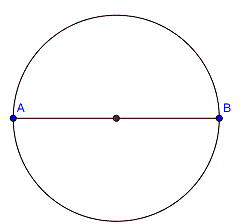
Die Antwort ist wirklich verblüffend: Der Punkt C muss irgendwo auf dem sogenannten "Thaleskreis" liegen. Das ist der Kreis, den man über der Strecke [AB] schlägt, indem man in der Mitte von [AB] einsticht und den Zirkel bis zu einem der Punkte öffnet. |
|||||||||||||||||||||||||
|
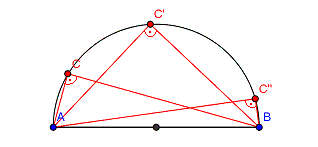
Wirklich an jeder beliebigen Stelle des Thaleskreises ergibt sich ein rechter Winkel, egal ob weit oben oder irgendwo rechts oder links.
|
|||||||||||||||||||||||||
|
|||||||||||||||||||||||||
| Anwendung | |||||||||||||||||||||||||
|
Den Thaleskreis braucht man immer dann, wenn über einer Strecke ein rechter Winkel gefordert wird. Wo der Punkt C dann genau liegen soll (denn bis jetzt ja einfach irgendwo auf dem Thaleskreis), muss durch eine zweite Bedingung festgelegt werden.
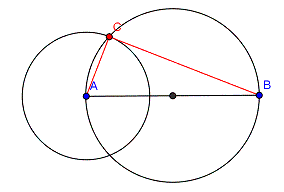
Beispiel: Erstelle ein rechtwinkliges Dreieck ABC über der Strecke [AB] mit AB = 5 cm mit einem rechten Winkel bei C, wobei der Abstand von A zu C 2 cm betragen soll. Der dritte Punkt C muss einerseits auf dem Thaleskreis liegen, andererseits auf einem Kreis von 2 cm um A. Beide Bedingungen legen seine Lage genau fest. |
|
||||||||||||||||||||||||
|
Im Prinzip gibt es unterhalb der Strecke [AB] noch einen zweiten Punkt, der beide Bedingungen erfüllt, allerdings passt dann die Benennung ABC gegen den Uhrzeigersinn (mathematische Zählrichtung) nicht mehr.
|
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Tangenten, Sekanten und Passanten | |||||||||||||||||||||||||
|
Geraden, die einen Kreis passieren, ohne ihn zu berühren, nennt man Passanten.
Geraden, die einen Kreis schneiden (logischer Weise in genau 2 Punkten), nennt man Sekanten. Und Geraden, die einen Kreis nur in einem Punkt berühren, nennt man Tangenten. |


|
||||||||||||||||||||||||
|
Die wichtigsten Eigenschaften von Tangenten sind:
1. In jedem Punkt eines Kreises gibt es immer nur eine einzige Tangente. Wenn man die Gerade ein wenig kippt, sieht es zwar immer noch so aus, als sei es eine Tangente, aber in Wirklichkeit schneidet sie den Kreis jetzt in zwei Punkten, oder berührt ihn an einer anderen Stelle. 2. Eine Tangente steht in ihrem Berührpunkt immer im rechten Winkel auf dem Radius. |
|||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||
| Tangenten konstruieren | |||||||||||||||||||||||||
|
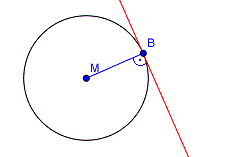
1. Tangente an Kreispunkt:
Damit ist auch klar, wie man eine Tangente an einen vorgegebenen Punkt auf der Kreislinie konstruiert: Man zeichnet den Radius an diesem Punkt ein, also die Strecke vom Mittelpunkt bis zu dem vorgegebenen Punkt. Und zeichnet dann die Senkrechte auf den Radius, die durch diesen Punkt geht. |
 
Zweimal senkrecht
ist parallel! 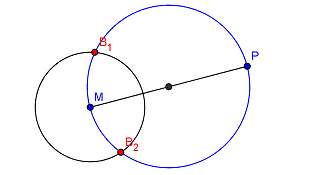 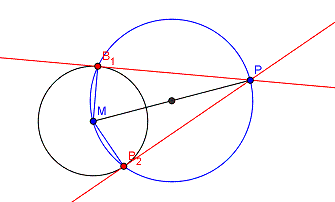
|
||||||||||||||||||||||||
|
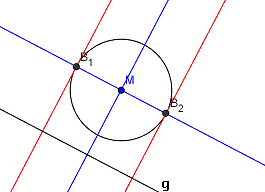
2. Tangente parallel zu Gerade
Manchmal wird der Berührpunkt nicht vorher angegeben. Stattdessen soll die Tangente so gezeichnet werden, dass sie parallel zu einer vorgegebenen Geraden verläuft. 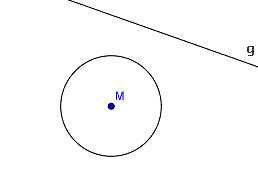 In diesem Fall muss man zunächst den Berührpunkt finden. Dazu zeichnet man eine Senkrechte auf die Gerade, die durch den Mittelpunkt des Kreises geht (blau). Wo diese Senkrechte die Kreislinie schneidet, findet man zwei Berührpunkte. Nun werden die Tangenten wie gehabt an diese Berührpunkte gezeichnet, also die Senkrechten auf die gerade konstruierte Senkrechte. :O) |
|||||||||||||||||||||||||
|
3. Tangente senkrecht zu Gerade
Eine andere Aufgabenvariante besteht darin, die Tangente(n) so an den Kreis zu zeichnen, dass sie nicht parallel, sondern senkrecht zu einer vorgegebenen Geraden verlaufen. 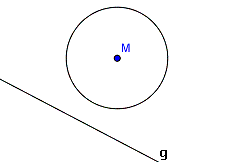 Wieder müssen wir den Berührpunkt selbst finden. Wir könnten nun eine Senkrechte auf die Gerade g mit dem Geodreieck so verschieben, dass sie den Kreis berührt. Viele Lehrer lassen diese Methode aber nicht zu, weil man den Berührpunkt so nur sehr ungenau findet, vor allem bei großen, "flachen" Kreisen. Stattdessen zeichnen wir wieder eine Senkrechte zu g, die durch den Mittelpunkt geht (blau). Dann eine zweite Senkrechte, die wieder durch M geht, und senkrecht zur ersten Senkrechten steht (blau). Jetzt haben wir eine exakte Parallele zu g gefunden. Auf den Schnittpunkten mit der Kreislinie liegen wieder die Berührpunkte. Nun nur noch die Tangenten zeichnen. |
|||||||||||||||||||||||||
|
4. Die Königsdisziplin: Tangente durch externen Punkt
Immer wieder gerne gefragt in Abschlussprüfungen: Zeichne von einem beliebigen Punkt P aus die Tangenten an einen Kreis. 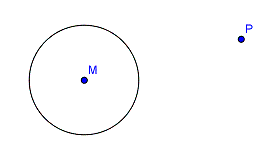 Die Lösung ergibt sich wieder durch die Überlegung, dass die Tangente im Berührpunkt senkrecht auf dem Radius stehen muss. Damit ergibt sich ein Dreieck aus M, P und dem Berührpunkt B, das "oben" bei B einen rechten Winkel haben muss. Erinnerst du dich? Thaleskreis! Wir müssen den Thaleskreis über der Strecke [MP] zeichnen. Dort wo der Thaleskreis unseren ursprünglichen Kreis schneidet, sind die Berührpunkte. |
|||||||||||||||||||||||||







