|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||||||||||||
|
Um Geometrie!
In den früheren Klassen hast du viel über geometrische Grundlagen wie Kreise, Linien, Winkel, Flächen und dreidimensionale Körper gelernt. In diesen Lektionen geht es nun darum, problemorientierter an die Sache heran zu gehen: Bei welchen Fragestellungen ergibt sich für den Stadtplaner ein Kreis? Unter welchen Bedingungen muss der Ingenieur eine Mittelsenkrechte einziehen? Warum bevorzugt der Innenarchitekt hier eine Winkelhalbierende? Wie findet der Gartenbauer den Mittelpunkt eines dreieckigen Grundstückes und was heißt hier überhaupt Mittelpunkt? |

Entspannung!!!
Diese und die folgenden Lektionen sind nicht besonders schwierig! |
||||||||||||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Kreislinie, Kreisinneres und Kreisäußeres | |||||||||||||||||||||||||||||||||||||||||||||||
|
Kreise ergeben sich immer dann, wenn man etwas über die Entfernung zu einem Punkt aussagt.
Sollen beispielsweise in einem Garten Blumen in einem Abstand von 2 m um einen Brunnen angepflanzt werden, so ergibt sich eine Kreislinie mit dem Radius 2 m um den Brunnen herum. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
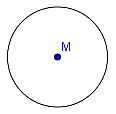
Die Kreislinie selbst ergibt sich, wenn man den Abstand zum Mittelpunkt auf einen Wert genau festlegt.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
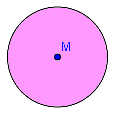
Das Kreisinnere ergibt sich, wenn der Abstand kleiner sein soll als ein vorgegebener Wert. Der Rasensprenger kann z.B. alle Stellen benetzen, deren Entfernung kleiner ist als 3,50 m.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
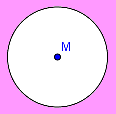
Das Kreisäußere ergibt sich, wenn der Abstand größer sein soll als ein vorgegebener Wert. Das Schaf hält z.B. eine Entfernung von mehr als 1,50 m zum Obstbaum ein, weil dieser durch einen Zaun geschützt ist.
|
|||||||||||||||||||||||||||||||||||||||||||||||
|
Ob man zum Kreisinnern oder zum Kreisäußeren auch noch die Linie dazurechnet, hängt von der genauen Fragestellung ab:
weniger als 2 m entfernt → Kreisinneres höchstens 2 m entfernt → Kreisinneres und Kreislinie mehr als 2 m entfern → Kreisäußeres mindestens 2 m entfernt → Kreisäußeres und Kreislinie |
|||||||||||||||||||||||||||||||||||||||||||||||
|
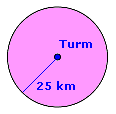
Anwendung:
Ein Fernsehturm soll mitten in einer Stadt aufgebaut werden. Welches Gebiet überstrahlt er, wenn die Fernsehwellen eine Reichweite von 25 km haben? Lösung: Er überstrahlt das Innere eines Kreises mit dem Radius von 25 km um den Turm als Mittelpunkt. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Die mathematische Schreibweise | |||||||||||||||||||||||||||||||||||||||||||||||
|
Natürlich ist das alles ein wenig zu einfach für den Mathematiker. Irgendetwas Schwieriges muss noch hinzu: Also hat er sich eine Kurzschreibweise für all das ausgedacht:
Kreislinie: k = {P | PM = r} Erklärung: PM bedeutet: Der Abstand zwischen P und M. Also liest man diese Zeile wie folgt: Die Kreislinie k ist die Menge aller Punkte P, für die gilt: Der Abstand der Punkte P zu M (dem Mittelpunkt) ist ein fester Wert r. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Die Mittelsenkrechte | |||||||||||||||||||||||||||||||||||||||||||||||
|
Ein Kreis ergibt sich, wenn alle Punkte den gleichen Abstand von EINEM Punkt haben.
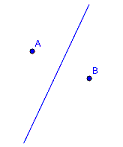
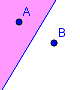
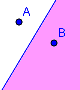
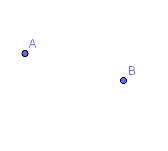
Eine Mittelsenkrechte ergibt sich, wenn alle Punkte den gleichen Abstand von ZWEI Punkten haben. Auf den Punkt genau in der Mitte von A und B kommt man sofort. Aber erkennst du auch, dass alle anderen Punkte auf der Mittelsenkrechten mAB ebenfalls den gleichen Abstand zu A und zu B haben – wenn auch einen größeren? |
|
||||||||||||||||||||||||||||||||||||||||||||||

Die Mittelsenkrechte selbst ergibt sich, wenn die Punkte genau den gleichen Abstand von A und B haben sollen.
Der Bereich auf der einen Seite der Mittelsenkrechten (=Halbebene) ergibt sich, wenn die Punkte näher an A als an B sind, die andere Seite ergibt sich, wenn die Punkte näher an B als an A sind. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
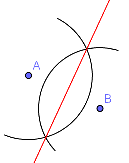
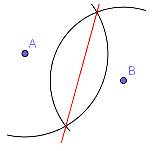
Wie konstruiert man die Mittelsenkrechte?
Mit dem Zirkel schlägst du einen Kreisbogen um den Punkt A. Dann schlägst du mit der gleichen Zirkelöffnung einen Kreisbogen um den Punkt B. Die beiden Punkte, in denen sich die Kreisbögen schneiden, verbindest du: Voilà – die Mittelsenkrechte! (Damit sich die beiden Kreisbögen überhaupt schneiden können, muss der Zirkel natürlich weiter geöffnet sein, als der halbe Abstand zwischen den beiden Punkten.) |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Anwendung:
Eine Hochspannungsleitung soll so zwischen den beiden Orten Alingen und Bedorf hindurchgeführt werden, dass sie gleich weit von beiden Orten entfernt ist. Lösung: Sie muss auf der Mittelsenkrechten zwischen den beiden Orten verlaufen. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||
| Der Umkreis | |||||||||||||||||||||||||||||||||||||||||||||||
|
Ein Kreis ergibt sich, wenn alle Punkte den gleichen Abstand von EINEM Punkt haben.
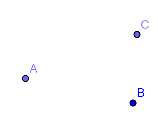
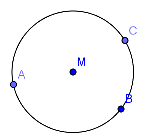
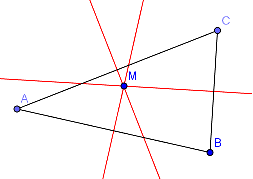
Eine Mittelsenkrechte ergibt sich, wenn alle Punkte den gleichen Abstand von ZWEI Punkten haben. Der Mittelpunkt des Umkreises ist der Punkt, der den gleichen Abstand von DREI Punkten hat. Wenn du den Zirkel in diesem Punkt einstichst, liegen alle drei vorgegebenen Punkte auf dem Kreis. Der Kreis liegt also um das aufgespannte Dreieck herum. |
|
||||||||||||||||||||||||||||||||||||||||||||||
|
Wie konstruiert man den Umkreis?
Du musst für alle drei Verbindungslinien die Mittelsenkrechte erstellen. Wo sich die drei Mittelsenkrechten schneiden, ist der Umkreismittelpunkt. Du findest den Mittelpunkt bereits mit zwei Mittelsenkrechten. Die dritte zeigt einem dann, ob man bei den ersten beiden einen Fehler gemacht hat. |
|||||||||||||||||||||||||||||||||||||||||||||||
|
Anwendung:
Ein Gärtner möchte möglichst genau in der Mitte zwischen drei Blumenbeete einen Teich anlegen. Wie findet er den richtigen Platz? Lösung: Er sucht den Umkreismittelpunkt der drei Punkte. |
|||||||||||||||||||||||||||||||||||||||||||||||







