|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||
|
Terme sind Formeln! Formeln um irgendetwas zu berechnen. Zum Beispiel wie viele Ziegel der Dachdecker braucht, wenn ein Dach x m2 groß ist. Wie lange eine Rakete braucht, um einen Planeten zu erreichen, der x km entfernt ist. Oder wie viel kg Futter man braucht, um ein Tierheim mit x Hunden oder Katzen zu versorgen. |
 |
||||||||||||||||||||||||||||||
|
Immer wenn man etwas berechnen möchte, benutzt man eine passende Formel dazu. Um solche Formeln geht es in diesem Kapitel. Allerdings sagt der Mathematiker nicht Formel dazu, sondern Term.
|
|||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Eine einfache Rechnung oder eine Formel? | |||||||||||||||||||||||||||||||
|
Braucht man Formeln (Terme) wirklich? Schließlich können wir schon seit der vierten Klasse vernünftig rechnen. Wozu denn nun auch noch Formeln?
Der Unterschied liegt darin, dass eine einfache Rechnung nur für einen einzigen Fall gilt. Eine Formel beschreibt hingegen alle Fälle eines Problems. |
Terme sind Formeln!
Die Mathematiker sind Künstler im Verschleiern allzu einfacher Tatsachen. 
|
||||||||||||||||||||||||||||||
|
Nehmen wir zum Beispiel das Tierheim. Wenn ein einzelner Hund im Durchschnitt 1,2 kg Futter pro Tag benötigt, dann brauchen wir für 20 Hunde:
20 · 1,2 kg = 24 kg Futter pro Tag. Das ist eine einfache Rechnung. Sie ist richtig für diesen einen Fall, dass das Tierheim 20 Hunde hat. Eine Formel ist etwas anderes: Sie erklärt, wie man für jede Anzahl von Hunden das Futter berechnet: x · 1,2 kg Für x setzt man die Anzahl der Hunde ein. |
|||||||||||||||||||||||||||||||
|
Alles klar? Terme sind überhaupt nicht schwer!
|
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| So sehen Terme aus | |||||||||||||||||||||||||||||||
|
Terme sind Formeln, also Rechenvorschriften, um irgendetwas zu berechnen. Weil sie ja für alle Fälle eines Problems gelten sollen, brauchen sie eine Variable, in die man unterschiedliche Zahlen einsetzen kann.
Meistens nimmt man als Variable x. Früher war es ein Platzhalter, also ein Leerraum, ein Strich __ oder ein Kästchen. Ab heute: x. (Oder y usw.) |
Ohne Variable macht eine Formel keinen Sinn.
|
||||||||||||||||||||||||||||||
|
Hier ein paar Beispiele:
|
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Einsetzungen und Termwerte | |||||||||||||||||||||||||||||||
|
Jede Formel bringt unterschiedliche Ergebnisse, je nachdem, welche Zahl man für die Variable einsetzt.
Die Formel 3x + 7 liefert 13, wenn ich 2 für x einsetze und 22, wenn ich 5 für x einsetze. Was man einsetzt nennt man Einsetzung. Was rauskommt, heißt Termwert. x = 2 → 3 · 2 + 7 = 13 x = 5 → 3 · 5 + 7 = 22 |

|
||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Die Definitionsmenge | |||||||||||||||||||||||||||||||
|
Zu einem Term bekommst du normalerweise auch eine Definitionsmenge gesagt.
Die Definitionsmenge legt fest, welche Zahlen du überhaupt einsetzen darfst. In die Hundefutterformel: x · 1,2 solltest du zum Beispiel NICHT alle möglichen Zahlen einsetzen. Du kannst zwar 4,5 · 1,2 rechnen, aber 4,5 Hunde??? Sinnvoll sind hier nur die natürlichen Zahlen. Deshalb ist die Definitionsmenge D: D = N |

|
||||||||||||||||||||||||||||||
|
Sollen nur einzelne Zahlen eingesetzt werden, gibt man die Definitionsmenge in Klammern an:
z.B. D = {3; 5; 7; 9} |
|||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||
| Die Wertetabelle | |||||||||||||||||||||||||||||||
|
Möchte man gleich für mehrere Einsetzungen die Werte der Formel berechnen, erstellt man lieber eine Tabelle, als alle Werte einzeln aufzuschreiben.
|
So eine Wertetabelle sieht nach nicht viel aus, aber oft steckt viel Arbeit dahinter, bis man alle Werte berechnet hat.
|
||||||||||||||||||||||||||||||
|
In der Wertetabelle schreibt man oben die Einsetzungen hin, darunter jeweils das, was raus kommt.
|
|||||||||||||||||||||||||||||||
|
Beispiel:
3·x + 7 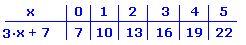
|
|||||||||||||||||||||||||||||||
|
Zunächst schreibst du oben die Zahlen hin, die du einsetzen sollst. Welche Zahlen das sind, steht normalerweise in der Aufgabe. Hier setzen wir 0 bis 5 ein.
Dann wird gerechnet: 3 · 0 + 7 = 7 Also die 7 unter die 0 schreiben. 3 · 1 + 7 = 10 Also die 10 unter die 1 schreiben. 3 · 2 + 7 = 13 Du schreibst die 13 unter die 2 u.s.w.. |
|||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||
| Graphische Auswertung | |||||||||||||||||||||||||||||||
|
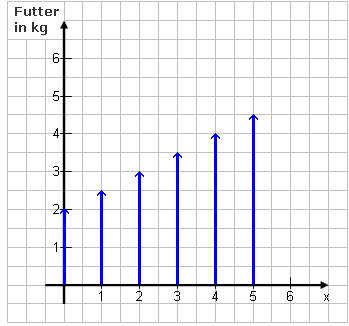
Zusätzlich zur Wertetabelle erstellt man oft noch eine Grafik für den Term. An einer Grafik erkennt man schnell die wichtigsten Eigenschaften eines Terms, wie etwa, ob die Werte ansteigen oder abfallen.
|

|
||||||||||||||||||||||||||||||
|
Eine Wertetabelle ist hingegen besser, wenn man die genauen Werte wissen möchte. Die kann man aus einer Grafik oft nur ungenau ablesen.
|
|||||||||||||||||||||||||||||||
|
Beispiel:
0,5 · x + 2 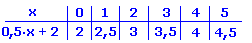
|
|||||||||||||||||||||||||||||||
|
So gehst du vor:
Zunächst zeichnest du eine waagerechte Achse für die Zahlen, die du einsetzt. An die Achse gehört rechts eine Pfeilspitze und ein x. Dann eine senkrechte für die Termwerte, die rauskommen. Wieder eine Pfeilspitze dran und die Bedeutung der Zahlen (z.B. Futter in kg). Nun nimmst du dir aus der Wertetabelle eine Einsetzung nach der anderen vor. |
|||||||||||||||||||||||||||||||
|
Nehmen wir als Beispiel x=2 und den zugehörigen Termwert von 3. Du gehst auf der x-Achse zu 2 und zeichnest an dieser Stelle einen Pfeil ein, der 3 hoch ist.
Auf die gleiche Art zeichnest du Pfeile für alle anderen x-Werte ein. Die Pfeile müssen immer so hoch sein wie der Termwert. |
|||||||||||||||||||||||||||||||
|
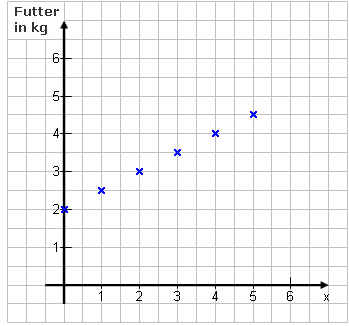
Statt die Pfeile zu zeichnen, kann man auch einfach dort, wo die Pfeilspitze endet, ein Kreuzchen machen.
|
|||||||||||||||||||||||||||||||








