mathepanik.de

Lektion
Gleichungen lösen

Worum geht es?

Eine Gleichung ergibt sich, wenn du einen Term hast, etwa

2 · x + 4

und dir jemand sagt, was bei deinem Term herauskommen soll. Etwa 7:

2 · x + 4 = 7

Du sollst nun herausfinden, welches x man einsetzen muss, damit die gewünschte Zahl herauskommt. Wie das geht, erfährst du hier.

In dieser Lektion lernst du

1.	Wie man vorgeht, um Gleichungen zu lösen.

2.	Was Äquivalenzumformungen sind.

3.	Einfache Gleichungen zu lösen.

4.	Die richtige Reihenfolge der Umformungen.

Wie man Gleichungen löst

2 · x + 4 = 7

Gleichungen sind Rätsel. Was muss ich für x einsetzen, damit 7 heraus kommt?

x = ???

Wir brauchen eine Methode, die immer funktioniert, bei einfachen und bei schwierigen Gleichungen.

Gleichungen sind Rätsel. Ich sage dir, was rauskommt, sag du mir, was man dazu eingesetzt hat.

Wahnsinnig schwierig!!! ;O)

So funktioniert es:

Man formt die Gleichung äquivalent um. Und zwar so, dass sie Schritt für Schritt einfacher wird.

Das bedeutet, dass man auf beiden Seiten der Gleichung die gleichen Rechnungen durchführt. Man addiert, subtrahiert, multipliziert oder dividiert auf beiden Seiten die gleiche Zahl.

In unserem Beispiel stört zunächst einmal die + 4. Um sie weg zu bekommen, rechnen wir auf beiden Seiten – 4.

2 · x + 4 = 7
2 · x + 4 – 4 = 7 – 4
2 · x = 3

Dadurch ändert sich zwar das Aussehen der Gleichung, nicht aber ihre Bedeutung.

Der Sinn davon ist, dass die Gleichung Schritt für Schritt einfacher wird. Bis man schließlich

x = ..... vor sich stehen hat.

Immer die Gegenoperation rechnen

Aber woher soll man wissen, welche Rechnung man braucht?

Man rechnet immer so, dass die Zahlen, die bei x stehen, verschwinden:


x + 6 = 15	Hier rechnet man – 6
x – 7 = 20	Hier rechnet man + 7
x · 3 = 24	Hier rechnet man : 3
x : 6 = 7	Hier rechnet man · 6

Du rechnest also immer die Gegenoperation! Statt Plus Minus, statt Minus Plus. Statt Mal Geteilt, statt Geteilt Mal.

Merke:

Führe immer die Gegenoperation durch:

	–	statt +			:	statt ·
	+	statt –			·	statt :

Äquivalenzumformungen

Solche Umformungen, die man auf beiden Seiten der Gleichung durchführt, heißen Äquivalenzumformungen.

Wir schauen uns die vier möglichen Arten zunächst an ganz einfachen Gleichungen an. Später werden wir sie miteinander kombinieren.

Die Rechnung, die man durchführt, schreibt man mit einem Kommandostrich hinter die Gleichung.

Es ist wie bei einer Waage, auf der ein Beutel mit unbekanntem Inhalt liegt und ein paar Münzen.

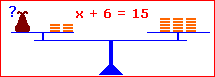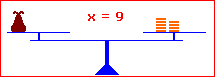1. Auf beiden Seiten das Gleiche subtrahieren:

x + 6 = 15 | – 6
x + 6 – 6 = 15 – 6
x = 9

2. Auf beiden Seiten das Gleiche addieren:

x – 7 = 20 | + 7
x – 7 + 7 = 20 + 7
x = 13

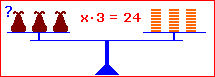
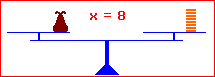
3. Auf beiden Seiten das Gleiche multiplizieren:

x · 3 = 24 | : 3
x · 3 : 3 = 24 : 3
x = 8

4. Auf beiden Seiten durch das Gleiche dividieren:

x : 6 = 7 | · 6
x : 6 · 6 = 7 · 6
x = 42

Die Lösungsmenge

Hat man die Gleichung durch äquivalente Umformungen so weit gebracht, dass

x = .... vor einem steht, ist man fertig.

Dieses x ist genau die Zahl, die man gesucht hat.

Deshalb präsentiert man die gesuchte Zahl in Form einer Lösungsmenge:

x : 6 = 7 | · 6
x : 6 · 6 = 7 · 6
x = 42 L = {42}

Die Reihenfolge der Umformungen

Nun sind Formeln aber oft nicht so einfach wie gerade gezeigt. Deshalb braucht man meistens mehrere Umformungsschritte, bis man x heraus bekommt.

Immer
zuerst Plus und Minus,
dann erst Mal und Geteilt!!!

Warum eigentlich?

Weil Punktrechnen vor Strichrechnen geht, "klebt" die 3 stärker an dem x als die 7. Die 3 ist näher am x als die 7. Deshalb müssen wir zuerst die äußere 7 entfernen, dann erst die innere 3.

2 · x + 4 = 7 | – 4
2 · x = 3 | : 2
x = 1,5 L = {1,5}

Auch nicht schwer! Die einzige Schwierigkeit besteht darin, sich die richtige Reihenfolge zu merken:

Zuerst Plus und Minus, dann erst Mal und Geteilt!

Weitere Beispiele:

4x – 7 = 19  | + 7
4x = 26  | : 4
x = 6,5 L = {6,5}

6 + 2x = 34 | – 6
2x = 28  | : 2
x = 14 L = {14}

x : 6 – 12 = -7  | + 12
x : 6 = 5  | · 6
x = 30 L = {30}

Fehler gefunden oder Anregungen?