|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | ||||||||||||||||||||||||||||||||
|
Prozent-Angaben kennt jeder: Milch mit 3,5% Fett. Ein Brot, das 30% Vollkornmehl enthält. Wein hat 13% Alkohol. Eine Partei bekommt bei den Wahlen 25% der Stimmen. Die Arbeitslosenquote liegt bei 10%.
Was man unter solchen Angaben versteht, lernen wir hier. |
 |
|||||||||||||||||||||||||||||||

|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Was ist ein Prozent? | ||||||||||||||||||||||||||||||||
|
Nichts Anderes als ein Bruch!!!!
Allerdings ein Bruch, der immer den gleichen Nenner hat: Den Nenner 100. 5% bedeutet:
30% bedeutet:
Statt Hundertstel schreibt man eben Prozent: % |

|
|||||||||||||||||||||||||||||||
|
Immer dann, wenn man ein Ganzes in mehrere Teile zerlegen möchte, verwendet man gerne Prozente, um zu beschreiben, wie groß die Teile sind.
Eine Tafel Schokolade besteht zum Beispiel aus 50% Zucker, 40% Fett, 9% Eiweiß und 1% sonstigen Stoffen (variiert je nach Sorte). Insgesamt kommen immer 100% heraus, also
|
||||||||||||||||||||||||||||||||
|
Der Vorteil im Vergleich zu Brüchen besteht darin, dass man besser vergleichen kann: 50% ist mehr als 40%. Bei Brüchen hätte man verschiedene Nenner, das macht das Vergleichen schwer:
Man könnte die Bestandteile der Schokolade natürlich auch als Kommazahl angeben: 0,5 Zucker, 0,4 Fett, 0,09 Eiweiß und 0,01 Sonstiges. Hört sich aber seltsam an. Prozentangaben sind da etwas angenehmer. |
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
| Brüche in Prozente umrechnen und umgekehrt | ||||||||||||||||||||||||||||||||
|
Bruch → Prozent:
Da Prozente Hundertstel-Brüche sind, muss man einfach nur den Bruch in Hundertstel umwandeln.
|
1 Ganzes = 100%
2 Ganze = 200%
Viele Brüche lassen sich nicht so einfach
in Prozent umwandeln, wie zum Beispiel
Wenn man unbedingt eine solche Umwandlung braucht, geht man besser den Umweg, aus dem Bruch zuerst eine Prozentzahl zu machen und daraus dann eine Prozentangabe. |
|||||||||||||||||||||||||||||||
|
Ein Ganzes sind immer 100%.
|
||||||||||||||||||||||||||||||||
|
Prozentangaben über 100% sind nicht sehr häufig, kommen ab und zu aber doch vor:
1
2
|
||||||||||||||||||||||||||||||||
|
Prozent → Bruch:
Rückwärts ist es genauso einfach. Man setzt statt der Prozente Hundertstel ein. Den Bruch, der dabei entsteht, muss man allerdings noch kürzen. 80% =
30% =
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Dezimalzahlen in Prozente umrechnen und umgekehrt | ||||||||||||||||||||||||||||||||
|
Kommazahl → Prozent:
Dezimalzahlen sind noch einfacher in Prozente anzugeben, als Brüche. Man verschiebt einfach nur das Komma um zwei Stellen nach rechts. 0,23 = 23% (Da 0,23 ja
|

|
|||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
|
Nun kann man auch unangenehme Brüche in Prozente umrechnen: Man wandelt sie einfach zunächst in Dezimalzahlen um:
|
||||||||||||||||||||||||||||||||
|
Prozent → Kommazahl:
Rückwärts, also von Prozentangabe zu Kommazahl ist es genauso einfach: Einfach das Komma um zwei Stellen nach links verschieben.
|
||||||||||||||||||||||||||||||||
|
||||||||||||||||||||||||||||||||
| Typische Prozentangaben | ||||||||||||||||||||||||||||||||
|
Die Bedeutung einiger Prozentangaben (also ihre Schreibweise als Bruch) solltest du auswendig können, da sie immer wieder auftauchen.
|
|
|||||||||||||||||||||||||||||||
|
100% = 1 200% = 2 etc.
25% =
10% =
1% =
|
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Balken- und Säulendiagramme | ||||||||||||||||||||||||||||||||
|
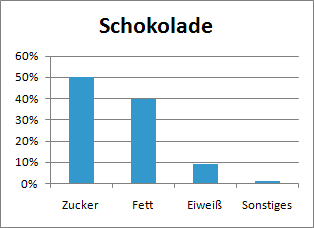
Wenn man Säulendiagramme (senkrecht) und Balkendiagramme (waagerecht) für Prozentangaben verwendet, geht es meistens darum, eine Sache in mehrere Bestandteile zu zerlegen, wie oben bei der Schokolade.
Deshalb ist die Summe aller Prozentangaben im Diagramm normalerweise 100%. |
 |
|||||||||||||||||||||||||||||||
|
Wenn wir berechnen müssen, wie hoch eine Säule für eine bestimmte Prozentangabe sein muss, brauchen wir einen Maßstab. Der sagt uns, wie hoch 1% oder 10% sind. Entsprechend müssen wir dann teilen oder multiplizieren.
10% ≙ 1 cm → 38% ≙ 1 cm · 3,8 = 3,8 cm |
||||||||||||||||||||||||||||||||
|
|
||||||||||||||||||||||||||||||||
| Kreisdiagramme und Kuchendiagramme | ||||||||||||||||||||||||||||||||
|
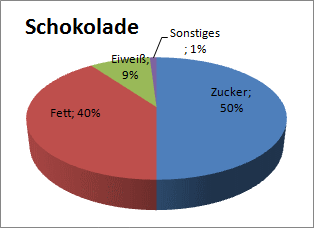
In Kreisdiagrammen (zweidimensional) oder Kuchendiagrammen (dreidimensional) ist die Aufteilung einer Sache in Bestandteile besonders gut zu sehen. Wieder müssen alle Teile zusammen 100% ergeben, so dass der Kreis oder der Kuchen komplett wird.
|
|
|||||||||||||||||||||||||||||||
|
Wenn man selbst ein Kreisdiagramm zeichnen soll, muss man die Prozentangaben in Grad umrechnen.
100% sind dann 360°. Also der ganze Kreis. |
||||||||||||||||||||||||||||||||
|
Wie viel Grad hat dann ein Kreissektor von 38%?
So etwas berechnest du mit dem Dreisatz:
|
||||||||||||||||||||||||||||||||








