|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||||||||||||||||
|
Wenn drei Flaschen Cola 2,40 € kosten, was kosten dann 7 Flaschen?
Das lässt sich sehr leicht berechnen, weil jede Flasche Cola das gleiche kostet. Mit jeder zusätzlichen Flasche werden die Kosten deshalb um den gleichen Betrag größer. Man sagt: Die Kosten steigen direkt proportional mit der Anzahl der Flaschen. Um Zusammenhänge, die sich auf diese einfache Weise berechnen lassen, geht es in dieser Lektion. |
 |
||||||||||||||||||||||||||||||||||||

|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| Was bedeutet "direkt proportional"? | |||||||||||||||||||||||||||||||||||||
|
Die Bezeichnung "direkt proportional" hört sich sehr kompliziert an. Gemeint ist aber genau das Gegenteil: Hier geht es um Zusammenhänge, die sich auf einfachste Art berechnen lassen.
Wie etwa die Kosten, die bei 7 Flaschen Cola entstehen. Mit jeder zusätzlichen Flasche werden die Kosten um den gleichen Betrag größer. Das macht die Berechnung besonders einfach. |
Direkte
Proportionalitäten sind die einfachsten mathematischen Zusammenhänge.

|
||||||||||||||||||||||||||||||||||||
|
Wenn ich doppelt so viele Flaschen kaufe, muss ich doppelt so viel bezahlen. Kaufe ich dreimal so viele Flaschen, muss ich dreimal so viel bezahlen.
Zwei Größen, sind dann direkt proportional zueinander, wenn sich aus einer Verdopplung der einen Größe (Flaschen) auch eine Verdopplung der anderen Größe (Kosten) ergibt. Aus einer Verdreifachung der einen Größe ergibt sich eine Verdreifachung der anderen, u.s.w. |
|||||||||||||||||||||||||||||||||||||
|
Auch wenn sich das Wort Proportionalität recht kompliziert anhört, freut man sich normalerweise, wenn etwas direkt proportional ist. Denn dann lassen sich unbekannte Größen (Kosten für Flaschen) auf einfachste Weise berechnen.
Stell dir vor, der Preis pro Flasche bliebe nicht gleich sondern würde mit jeder weiteren Flasche ein wenig billiger. Das wäre unglaublich kompliziert zu rechnen! |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
| Beispiele für direkte Proportionalitäten | |||||||||||||||||||||||||||||||||||||
|
Immer dann, wenn du etwas einkaufst, und der Preis pro Portion (pro Flasche, pro kg, pro Tüte etc.) gleich bleibt, hast du es mit einer direkten Proportionalität zu tun. Sehr gut! Die Rechnung ist einfach!
Gibt es allerdings Rabatt, also einen Preisnachlass ab einer bestimmten Menge, ist es keine direkte Proportionalität mehr. Doppelt so viel von der Sache kostet dann nicht mehr doppelt so viel Geld. Es wird zwar billiger aber schwieriger zu rechnen. |
Wenn man doppelt so viel lernt, bekommt man leider nicht automatisch auch eine doppelt so gute Note.
Keine direkte Prop. :O{ |
||||||||||||||||||||||||||||||||||||
|
Wenn ein Auto mit gleicher Geschwindigkeit fährt, ist die Anzahl der gefahrenen Kilometer direkt proportional zur gefahrenen Zeit.
Ändert es jedoch seine Geschwindigkeit, liegt keine direkte Proportionalität mehr vor. Und die Rechnungen werden wieder schwieriger. |
|||||||||||||||||||||||||||||||||||||
|
Handy-Tarife sind nur dann direkt proportional, wenn sie keine Grundgebühr haben. Dann musst du für doppelt so viel Sprechzeit am Ende des Monats auch doppelt so viel Geld bezahlen.
|
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| Wertetabelle und grafische Darstellung | |||||||||||||||||||||||||||||||||||||
|
Um sich einen Überblick zu verschaffen, rechnet man normalerweise ein paar Werte aus und schreibt sie in eine Wertetabelle.
Anschließend lohnt es sich meistens auch, sie als Grafik darzustellen. Denn an einer Grafik lässt sich der grobe Verlauf besonders gut erkennen. |

|
||||||||||||||||||||||||||||||||||||
|
Nehmen wir als Beispiel einen Handy-Tarif ohne Grundgebühr. Die Minute soll 40 Cent kosten.
Wie hoch die Kosten nach einer gewissen Anzahl von Gesprächs-Minuten sind, kann man sich leicht durch Multiplikation errechnen und in eine Wertetabelle eintragen. 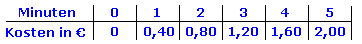
|
|||||||||||||||||||||||||||||||||||||
|
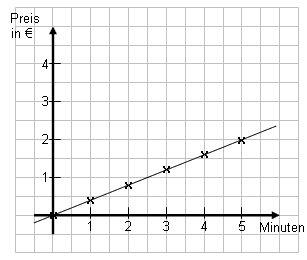
Zum Schluss erstellen wir eine Grafik. Die Größe, von der man ausgeht (hier die Anzahl der Minuten), wird nach rechts eingezeichnet, das was man berechnet (hier die Kosten), zeichnet man nach oben ein.
In der Grafik rechts siehst du das Ergebnis. |
|||||||||||||||||||||||||||||||||||||
|
Wie du siehst, ergibt sich eine Gerade, die durch den Ursprung geht.
Dies ist typisch für direkte Proportionalitäten! Wenn man sie zeichnet, erhält man immer Geraden, die durch den Ursprung gehen. |
|||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||
| Der Proportionalitäts-Faktor | |||||||||||||||||||||||||||||||||||||
|
Wenn ein Zusammenhang direkt proportional ist, dann, steigt die berechnete Größe immer um den gleichen Betrag, wenn man Eins mehr einsetzt.
Die Kosten beim Handy steigen mit jeder Minute um 0,40 €. Die Kosten für die Cola steigen mit jeder weiteren Flasche um 0,80 €. Wenn ein Auto gleichmäßig 60 km pro Stunde fährt, steigt die gefahrene Strecke mit jeder weiteren Stunde um 60 km. |

|
||||||||||||||||||||||||||||||||||||
|
Diesen Anstieg nennt man Proportionalitäts-Faktor.
Beim Handy ist der Proportionalitäts-Faktor der Preis pro Minute. Bei der Cola der Preis pro Fasche. Bei Fleisch oder Obst der Preis pro Kilogramm. Beim Auto die Kilometer pro Stunde. |
|||||||||||||||||||||||||||||||||||||
|
Berechnung:
Um den Proportionalitäts-Faktor zu ermitteln, teilt man den berechneten Wert durch den eingesetzten Wert! |
|||||||||||||||||||||||||||||||||||||
|
Beispiele:
3 Flaschen Cola kosten 2,40 €. Proportionalitäts-Faktor: 2,40 € : 3 = 0,80 € 12 Gesprächsminuten kosten 4,20 €. Proportionalitäts-Faktor: 4,20 € : 12 = 0,35 € Für 200 km braucht man 2,5 Stunden. Proportionalitäts-Faktor: 200 km : 2,5 h = 80 km/h |
|||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||
| Quotientengleichheit | |||||||||||||||||||||||||||||||||||||
|
Wenn du einen berechneten Wert durch den zugehörigen eingesetzten Wert teilst, erhältst du den Proportionalitäts-Faktor. Egal welches Paar von Werten du nimmst. Es ist also egal, ob man dir sagt, dass 3 Flaschen 2,40 € kosten, oder dass 4 Flaschen 3,20 € kosten. Es kommt immer der gleiche Flaschenpreis heraus.
|

|
||||||||||||||||||||||||||||||||||||
|
Statt "Teilen" kann man auch sagen, dass man den Quotienten von zwei Werten bildet. Deshalb gilt:
Bei einer direkten Proportionalität sind alle Wertepaare quotientengleich. Sobald du Rabatt bekommst oder etwas aus anderen Gründen nicht direkt proportional ist, sind die Paare nicht mehr quotientengleich. |
|||||||||||||||||||||||||||||||||||||
|
Beispiel:
Untersuche, ob dieses Auto gleichmäßig gefahren ist, ob also Kilometer und Fahrzeit direkt proportional zueinander sind. 
|
|||||||||||||||||||||||||||||||||||||
|
Wir bilden Quotienten aus den einzelnen Wertepaaren.
140 km : 2 h = 70 km/h 350 km : 5 h = 70 km/h 540 km : 8 h = 70 km/h 780 km : 12 h = 65 km/h Ergebnis: Das Auto fährt nur 8h lang gleichmäßig. Über die ganze Fahrzeit betrachtet liegt keine direkte Proportionalität vor. |
|||||||||||||||||||||||||||||||||||||








