| Worum geht es? |
Hast du schon einmal 2
Euro in einem Geschäft bezahlt? Kennst du jemanden, der 1
m groß ist oder 40
kg wiegt? :O) Nein! Einige Brüche haben wir zwar ganz gut im Gefühl, wie ein Halb, drei Viertel oder ein Achtel. Aber im Alltag nimmt man doch für die allermeisten Probleme lieber Kommazahlen, um einen Bruchteil auszudrücken: 2,75 €; 1,63 m; 40,33 kg.
|
|
|

| In dieser Lektion lernst du: |
|
| 1. | Was Dezimalzahlen sind und wie man sie schreibt. |
|
| 2. | Wie man eine Dezimalzahl in einen Bruch umrechnet und umgekehrt. |
|
| 3. | Und was es mit den Nullen am Ende auf sich hat. |
|
|
|
|
|
|
| Die dezimale Schreibweise |
|
Wir kennen Kommazahlen vom Einkaufen her: 4,99 €.
Weil 100 Cent einen Euro ergeben, verwenden wir zwei Stellen hinter dem Komma. 0 bis 99 Cent passen da hinein.
In anderen Fällen, wenn es nicht ums Geld geht, braucht man oft nur eine Stelle: 6,7 kg
Oder aber mehr Stellen hinter dem Komma: 34,6138 m2.
|
|
|
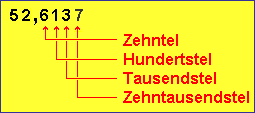
Und das funktioniert so:Jede Stelle hinter dem Komma hat eine bestimmte Bedeutung: Die erste Stelle steht für Zehntel, die zweite für Hundertstel, dann Tausendstel, Zehntausendstel usw. 4,7 bedeutet: 4 Ganze und 7 Zehntel: 4
56,1 bedeutet: 56 Ganze und ein Zehntel: 56
|
|
3,75 bedeutet: 3 Ganze, 7 Zehntel und 5 Hundertstel. Da ein Zehntel aber gleichzeitig zehn Hundertstel sind, kann man auch alles hinter dem Komma in Hundertstel angeben: 3,75 = 3
1,28 = 1
|
|
Und so geht es weiter: 6,123 = 1
0,4405 =
450,3 = 450
|
|
|
|
|
| Umrechnen: Von der Kommazahl zum Bruch |
|
Wie man aus einer Kommazahl wieder einen richtigen Bruch oder eine gemischte Zahl erzeugt, hast du gerade gesehen.
Worauf man allerdings achten muss, ist, dass man eventuell zum Schluss noch kürzen kann.
|
|
|
0,71 =
4,531 = 4
1,2 = 1
= 1
8,5 = 8
= 8
36,25 = 36
= 36
|
|
|
|
|
| Umrechnen: Vom Bruch zur Kommazahl |
|
Jetzt wird's etwas schwieriger: Man gibt uns einen Bruch und wir sollen ihn als Kommazahl schreiben.
|
|

Vielleicht wirst du schon misstrauisch?? Das klappt doch nie im Leben für alle Nenner!!! Wie bitte schön soll ich
in Zehntel oder Hundertstel umwandeln? Wie man das macht, lernen wir erst beim Dividieren von Kommazahlen.
|
Einfach ist es, wenn der Bruch bereits in Zehntel, Hundertstel oder Tausendstel angegeben wurde:
= 0,4
= 2
= 2,3
= 4
= 4,78
|
|
|
Schwieriger wird es, wenn der Bruch einen anderen Nenner hat. Dann muss man den Nenner durch Kürzen und Erweitern auf 10, 100, 1000 usw. bringen.
|
|
|
|
|
=
=
= 0,75 2
= 2
= 2
= 2,06
=
=
= 0,3
|
|
|
|
|
| Die Sache mit den Nullen am Ende |
|
Der eine Fisch wiegt 1,6 kg, der andere 1,60 kg und da liegt auch noch ein dritter auf dem Tisch, mit einem Gewicht von 1,600 kg.
Du ahnst es: Alles das Gleiche!
|
|
Endnullen kann man weglassen oder hinschreiben.
|
|
Manchmal mag man gerne ein paar Nullen anhängen, damit es schöner aussieht. 1,600 kg zeigt schön, dass es sich hinter dem Komma um 600 Gramm handelt. Deshalb ist es bei Gewichtsangaben üblich, 3 Stellen anzugeben, selbst dann, wenn sie leer sind.
Bei Geld ist es üblich, zwei Nachkommastellen anzugeben, auch dann, wenn sie leer sind:
3,40 € 7,00 €
|
|
|
Für die Zahl machen die Endnullen keinen Unterschied. Man kann sie angeben oder auch nicht.
|
|