|
|
| Hilfe |
| Diskutieren |
| Panik-Test |
| Themenübersicht |
| zu den Übungsaufgaben |
| Worum geht es? | |||||||||||||||||||||||
|
Hat man zwei Kommazahlen, kann man sofort sagen, welche größer ist. Das ist genauso leicht, wie wenn man zwei normale Zahlen miteinander vergleicht.
Außerdem geht es in dieser Lektion ums Runden. Runden bedeutet – wie bei normalen Zahlen auch – dass man eine Zahl nicht genau, sondern nur ungefähr angibt. Auch nicht schwierig, versprochen! |
 |
||||||||||||||||||||||

|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
| Dezimalzahlen vergleichen | |||||||||||||||||||||||
|
Ist 3,399 kleiner oder größer als 3,41???
Dezimalzahlen vergleicht man genauso wie normale Zahlen: Man schaut sich bei beiden Zahlen von links nach rechts die einzelnen Stellen an. Die Zahl, die zuerst eine größere Ziffer an der jeweiligen Stelle hat, ist die größere. Deshalb ist: 3,399 < 3,41 Die Einer sind bei beiden noch gleich, aber bei den Zehntel hat die erste Zahl eine 3, die zweite Zahl eine 4. Dass später bei der ersten Zahl noch zwei Neunen kommen, spielt keine Rolle. |
Die erste Ziffer, die größer ist, gewinnt!

|
||||||||||||||||||||||
|
Beispiele:
0,007 > 0,0008 Weil die erste Zahl bei den Tausendstel eine 7 hat und die zweite Zahl nur eine 0. Die anderen Ziffern zuvor waren noch gleich. 23,827 < 23,831 Bei den Hundertstel hat die erste Zahl eine 2, die zweite Zahl eine 3. 18,9 > 18,888 Bei den Zehntel gewinnt die 9 gegen die 8. Dass die zweite Zahl noch mehr Nachkommastellen hat, spielt natürlich keine Rolle. |
|||||||||||||||||||||||
|
|||||||||||||||||||||||
| Dezimalzahlen runden | |||||||||||||||||||||||
|
Runde 23,31 auf Zehntel.
Beim Runden sagt man uns immer, auf welche Stelle wir runden sollen: Auf Zehntel, auf Hundertstel, auf Tausendstel. Vielleicht aber auch auf Einer oder Zehner. Wir geben die Zahl dann nur noch mit dieser gewünschten Genauigkeit an: 23,31 ≈ 23,3 Die restlichen Ziffern schneiden wir ab. |
Runden muss man sehr häufig, weil Dezimalzahlen oft unnötig genau sind.
Wenn du Turnschuhe kaufen möchtest und diese 47,99 € 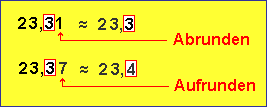

|
||||||||||||||||||||||
|
Dabei können wir abrunden oder aufrunden.
Um zu entscheiden, ob wir ab- oder aufrunden, sehen wir uns die nächste Ziffer an, also die, ab der wir anschließend abschneiden. Ist sie kleiner als 5, wird abgerundet, Ist sie größer oder gleich 5, wird aufgerundet. Abrunden heißt, wir lassen die letzte Ziffer, die wir schreiben, so wie sie ist. Aufrunden heißt, wir machen die letzte Ziffer eins größer.
|
|||||||||||||||||||||||
|
Beispiele:
Runde auf Hundertstel:
|
|||||||||||||||||||||||
|
Runde auf Tausendstel:
|
|||||||||||||||||||||||
|
|
|||||||||||||||||||||||
| Runden mit Überlauf | |||||||||||||||||||||||
|
Beim Aufrunden (nicht beim Abrunden) kann es zu einem Überlauf kommen, wenn die Stelle, auf die gerundet wird, eine 9 enthält.
|
Muss eine
9 aufgerundet werden, entsteht ein Überlauf! |
||||||||||||||||||||||
|
Runde 3,396 auf Hundertstel.
Wegen der 6 wird aufgerundet. Dabei wird die 9 um Eins erhöht. Und dabei laufen die Hundertstel über. Aus der 3,39 wird also eine 3,40 oder, anders geschrieben, eine 3,4. |
|||||||||||||||||||||||
|
Runde 27,995 auf Hundertstel.
Wegen der 5 wird aufgerundet, die 9 kriegt Eins dazu, läuft über, die 9 davor läuft deshalb auch über und wir erhalten: 28 ! |
|||||||||||||||||||||||







