mathepanik.de

Lektion
Dezimalzahlen dividieren

Worum geht es?

Dieses Mal ein eher schwieriges Thema!

Zum Einen ist das schriftliche Teilen schon bei normalen Zahlen nicht so einfach. Da können sich jede Menge Fehler einschleichen.

Wenn man nun aber Dezimalzahlen teilen möchte, kommt auch noch das Komma hinzu, was das Problem leider noch ein wenig komplizierter macht.

Also: Radio abschalten, aus allen Chats rausgehen und super konzentrieren! Sonst hast du keine Chance.

In dieser Lektion lernst du:

1.	Wie man durch 10, 100, 1000 etc. teilt.

2.	Wie man eine Kommazahl durch eine natürliche Zahl teilt.

3.	Wie man eine Kommazahl durch eine andere Kommazahl teilt.

4.	Wie man natürliche Zahlen teilt ohne Rest.

5.	Und wie man durch Teilen jeden beliebigen Bruch in eine Kommazahl umwandeln kann.

Durch 10, 100, 1000 etc. teilen

Super einfach:

Durch 10, 100, 1000 etc. (Stufenzahlen) dividierst du, indem du einfach nur das Komma um die entsprechende Anzahl von Stellen verschiebst.

Also genauso wie beim Multiplizieren, nur in die andere Richtung:

Nach links
oder nach rechts?

Überlege dir einfach, ob die Zahl kleiner oder größer werden muss.

: 10	ist das Gleiche wie · 0,1
: 100	ist das Gleiche wie · 0,01

: 0,1	ist das Gleiche wie · 10
: 0,01	ist das Gleiche wie · 100

345,6	: 100	= 3,456
67,33	: 100	= 0,6733
4,6	: 1000	= 0,0046

Soll man durch 0,1 ; 0,01 ; 0,001 etc. dividieren, verschiebt man das Komma in die andere Richtung:

0,005	: 0,01	= 0,05
2,34	: 0,1	= 23,4
0,34	: 0,001	= 340

Kommazahl durch natürliche Zahl

Wie man natürliche Zahlen durch andere natürliche Zahlen teilt, weißt du seit der dritten Klasse.

Bei Kommazahlen kommt nun die Frage hinzu, wo man im Ergebnis das Komma setzen muss. Dabei gilt NICHT die gleiche Regel wie beim Multiplizieren!!!

Sondern:	Da, wo du beim Dividieren das Komma überschreitest, setzt du das Komma auch im Ergebnis!

Merke:

	Kommazahl geteilt durch natürliche Zahl

	Da, wo du beim Dividieren das Komma überschreitest, setzt du das Komma auch im Ergebnis!

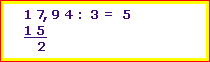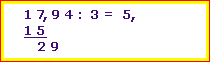
Beispiel: 17,94 : 3 = ???

Die 3 passt nicht in die 1. Sie passt aber in die 17, nämlich 5 mal. Also die 5 hinschreiben.

5 · 3 = 15. Unter die 17 schreiben. Bleiben 2.

Die 9 runter holen. ABER ACHTUNG! Hier überschreiten wir das Komma. Deshalb JETZT das Komma im Ergebnis setzen!

29 : 3 geht 9 mal. Hinschreiben. 9 · 3 sind 27. Unter die 29 schreiben. Bleiben wieder 2.

Die 4 runterholen. 24 : 3 = 8. Hinschreiben. 8 · 3 = 24. Unten hin, bleiben Null, fertig!

Beispiel 2:

2 0 8,2 : 6 = 3 4,7
1 8
0 2 8
0 2 4
0 0 4 2
0 0 4 2
0 0 0 0

Erst wenn du die letzte 2 herunter holen musst, überschreitest du das Komma. Genau dann setzt du es auch im Ergebnis.

Kommazahl durch Kommazahl

Wie verändert sich die Situation, wenn auch rechts eine Kommazahl steht? Wie geht man mit deren Komma um?

Gar nicht!

Man teilt nicht durch eine Kommazahl!!!
Das wäre höllisch kompliziert!

Merke:

	Man teilt nicht durch eine Kommazahl!

	Man verschiebt bei beiden Zahlen das Komma so, dass es bei der zweiten Zahl weg fällt.

Stattdessen schreibt man die Aufgabe um: Man verschiebt bei BEIDEN Zahlen das Komma soweit, dass die rechte Zahl natürlich wird, also kein Komma mehr hat.

Beispiele:


7,82 : 3,4	= 78,2 : 34	(um eine Stelle)
0,592 : 0,04	= 59,2 : 4	(um zwei Stellen)
65 : 1,6	= 650 : 16	(um eine Stelle)

Hat man die Aufgabe umgeschrieben, führt man die Division so durch, wie wir es oben gelernt haben.

8,6 4 : 3,6 =
8 6,4 : 3 6 = 2,4
7 2
1 4 4
1 4 4
0 0 0

Natürliche Zahlen teilen ohne Rest

Hat man früher durch eine Zahl geteilt, die nicht aufging, durfte man bis zur fünften Klasse einfach den Rest hinschreiben.

Das kannst du jetzt vergessen! Ab jetzt wird geteilt, bis die Socken qualmen! Sobald die natürliche Zahl "verbraucht" ist, setzt du im Ergebnis ein Komma und holst Endnullen runter, bis die Division fertig ist.

Das darf man, weil man sich jede natürliche Zahl auch als Kommazahl denken darf:

73 = 73,00000

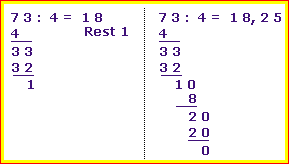
Im Beispiel rechts teilen wir ganz normal, bis die 3 herunter geholt worden ist und von 33 noch 1 übrig ist. Im Ergebnis haben wir 18 stehen. Früher hätten wir "Rest 1" hingeschrieben.

Ab heute setzen wir stattdessen im Ergebnis das Komma, denken uns die 73 als 73,000... und nehmen Endnullen herunter, bis das Teilen endlich aufgeht.

Beispiel 2:

5 1 : 8 = 6,3 7 5
4 8
0 3 0
0 2 4
0 0 6 0
0 0 5 6
0 0 0 4 0
0 0 0 4 0
0 0 0 0 0

Periodische Kommazahlen

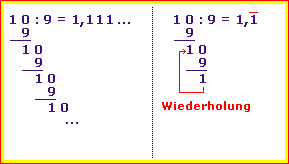
Beim Teilen ohne Rest kann etwas Unangenehmes passieren: Es hört nicht mehr auf.

1 0 : 9 = 1,1 1 1 ...
0 9
0 1 0
0 0 9
0 0 1 0

Das kann noch ewig so weiter gehen. Es dreht sich im Kreis, der Hund beißt sich in den eigenen Schwanz.

Eine ellenlange Lektion!!!! :O{

Ergebnis:
Eins Komma Periode Eins

In solchen Fällen sprechen wir von einer Periode.

Sobald ein Rest auftaucht, der schon einmal da war: Nicht weiterrechnen! Denn es wird sich alles so wiederholen, wie schon einmal. Stattdessen markiert man im Ergebnis die Wiederholung, die Periode, mit einem Strich.

Beispiel 2:

2 5 : 6 = 4,1 6 7
2 4
0 1 0
0 0 6
0 0 4 0
0 0 3 6
0 0 0 4

Wie man Brüche in Kommazahlen umwandelt

In der Lektion "Dezimalzahlen verstehen" haben wir gelernt, wie man einen Bruch in eine Kommazahl umwandelt – ABER nur für Brüche mit sehr angenehmen Nennern wie 4, 5, 8, 20 usw. Diese hat man durch Kürzen und Erweitern auf Zehntel, Hundertstel usw. gebracht und dann als Kommazahl geschrieben.

3 · 25

4 · 25

100

= 0,75

Merke:

	Bruch in eine Kommazahl umrechnen:


	Einfach nur den Zähler durch den Nenner teilen!

Da wir gerade gelernt haben, wie man ohne Rest teilt, können wir nun ALLE Brüche in Kommazahlen umwandeln.

Denn: Ein Bruchstrich bedeutet, was das Rechnen betrifft, einfach nur geteilt!!!

heißt: 3 geteilt durch 8.

Deshalb müssen wir einfach nur Zähler durch Nenner teilen und wie erhalten eine Kommazahl! :O)

Beispiele:

= 3 : 8

= 0,375

= 5 : 16

= 0,3125

= 5 : 6

= 0,83

= 3 : 11

= 0,27

= 1 : 7

= 0,142857

Fehler gefunden oder Anregungen?