| Worum geht es? |
In der nächsten Lektion werden wir Brüche addieren. Dazu brauchen wir eine Technik, die wir hier lernen: Brüche in eine andere Schreibweise umzuwandeln. Eine halbe Pizza ist genau das gleiche, wie zwei Viertel Pizzen.
ist also das Gleiche wie
oder auch wie
. Ebenso kann man statt
auch
oder
schreiben. Wie man von einer Schreibweise in die andere umrechnet, darum geht es hier.
|
|
|

| In dieser Lektion lernst du: |
|
| 1. | Wie man einen Bruch kürzt. |
|
| 2. | Wie man einen Bruch erweitert. |
|
|
|
|
|
|
| Wozu man die Umrechnung braucht |
|
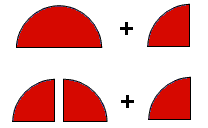
In der nächsten Lektion geht es ums Addieren von Brüchen. Wenn man eine Hälfte von einer Pizza bekommt und später noch einmal ein Viertel, wie viel hat man dann insgesamt erhalten?
|
|
|
Halbe und Viertel kann man nicht einfach so zusammen zählen, da sie ja unterschiedlich große Stücke sind. Stattdessen muss man sich überlegen, wie man die halbe Pizza in Viertel angeben kann: 2 Viertel natürlich. Anschließend kann man leicht addieren:
und
sind
. Man muss Brüche für solche Rechnungen oft in eine andere Form umschreiben. Die Techniken, mit denen man das tut – auch für schwierigere Brüche – heißen Kürzen und Erweitern.
|
|
|
|
|
| Das Kürzen von Brüchen |
Von "Kürzen" spricht man, wenn man einen Bruch einfacher schreibt, so dass er aus kleineren Zahlen besteht.
kann man z.B. kürzen zu
. Beide Brüche sind gleich, aber der zweite sieht einfacher aus, weil er kleinere Zahlen hat.
|
|
|
|
Wie kürzt man?
Man teilt den Zähler und den Nenner durch die gleiche Zahl!
|
|
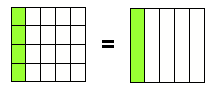
Beispiel 1: Schreibe
in Drittel.
=
Um aus der 12 im Nenner eine 3 zumachen, muss man durch 4 teilen. Deshalb teilen wir auch den Zähler durch 4. Man muss Zähler und Nenner immer durch die gleiche Zahl teilen!
=
=
|
|
Beispiel 2: Schreibe
in Fünftel.
=
Um aus 25 eine 5 zu machen, teilen wir Zähler und Nenner durch 5.
=
=
|
|
Beispiel 3:Kürze den Bruch
. (Damit ist gemeint, man soll ihn so einfach wie möglich schreiben.) Man könnte den Bruch durch 2 teilen. Dann bekäme man Achtel. Wir können ihn aber auch durch 4 teilen, dann erhalten wir Viertel. Mehr geht nicht, denn durch 8 teilen geht wegen dem Zähler nicht, und durch 6 scheitert am Nenner.
=
=
|
|
|
|
|
| Tricks |
Schrittweise KürzenManchmal erkennt man nicht gleich, durch welche Zahl man maximal teilen kann (mathematisch gesprochen wäre es der ggT, der größte gemeinsame Teiler). Dann kürzt man Schrittweise:
=
=
=
=
|
|
Die beste Zahl (der ggT von 54 und 72) wäre 18 gewesen. Aber zuerst durch 2 und dann durch 9, da kommt man leichter drauf, und das Ergebnis ist das Gleiche.
|
EintelBleibt nach dem Kürzen eine 1 im Nenner stehen, darf man den Bruch wieder als natürliche Zahl schreiben. Denn "Eintel" sind ja "Ganze".
= 3 ;
= 7 ;
=
= 9
|
|
|
|
|
| Das Erweitern von Brüchen |
Von "Erweitern" spricht man, wenn man einen Bruch komplizierter schreibt, so dass er aus größeren Zahlen besteht.
kann man z.B. erweitern zu
. Beide Brüche sind gleich, aber der zweite sieht komplizierter aus, weil er größere Zahlen hat. Auch wenn er komplizierter aussieht, braucht man ihn manchmal genau in dieser Form, z.B. wenn man ihn zu anderen Zehntel addieren möchte.
|
|
|
|
Wie erweitert man?
Man multipliziert den Zähler und den Nenner mit der gleichen Zahl!
|
|
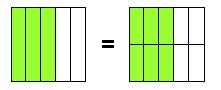
Beispiel 1: Schreibe
in Sechzehntel.
=
Um aus der 8 im Nenner eine 16 zumachen, muss man mit 2 malnehmen. Deshalb multiplizieren wir auch den Zähler mit 2.
=
=
|
|
Beispiel 2:Erweitere
auf Vierundzwanzigstel. Um von der 4 auf 24 zu kommen, müssen wir mit 6 malnehmen.
=
=
|
|
Beispiel 3:Erweitere
auf 84-stel. 84 : 7 = 12, also müssen wir Nenner und Zähler mit 12 malnehmen.
=
=
|
|
|
|
|
| Brüche vergleichen |
Ist ein Bruch größer oder kleiner als ein anderer? Besitzen beide den gleichen Nenner, ist das leicht zu entscheiden: Derjenige mit dem größeren Zähler ist größer, denn er hat ja mehr von den Bruchteilen.
<
;
<
|
|
|
Haben sie unterschiedliche Nenner aber den gleichen Zähler, ist es auch noch einfach: Beide haben gleich viele Bruchstücke, aber der mit dem kleineren Nenner hat die größeren Stücke!!! Deshalb ist er auch der größere.
<
;
<
|
|
Schwierig wird es, wenn Zähler und Nenner verschieden sind. Um sie überhaupt vergleichen zu können, kürzt oder erweitert man einen oder beide so, dass sie den gleichen Nenner haben.
?
Wir können beide auf den Nenner 24 bringen.
=
=
;
=
=
Jetzt wird es deutlich:
<
→
<
|
|